题目内容
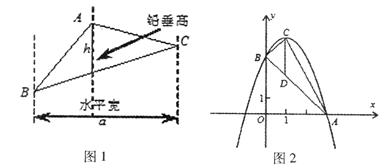
(本题12分)阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部的线段的长度叫△ABC的“铅垂高”(h).我们可行出生种计算三角形面积的新方示: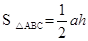 ,即三角形面积等于水平宽与铅垂高乘积的一半.
,即三角形面积等于水平宽与铅垂高乘积的一半.
解答下列问题:
如图2,抛物线顶点C(1,4),交x轴于点A(3,0),交y轴于点B.
(1)求抛物线和直线AB的解析式;
(2)求△ABC的铅垂高CD及S△ABC
(3)设点P是抛物线(在第一象限内)上的一个动点,是否存在一点P,使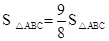 ,
,
若存在,求出P点的坐标;若不存在,请说明理由.
解:(1)设抛物线的解析式为:
把A(3,0)代入解析式得 a(3-1)2+4=0. 解得
所以 ……………………………………… 2分
设直线AB的解析式为:
由求得B点的坐标为
把,
代入
得
![]()
解得:
所以 …………………………………………………………… 4分
(2)因为C点坐标为(1,4)所以当x=1时, y2=2
所以CD=4-2=2 ……… 5分
………………………………………………………… 6分
(3)假设存在符合条件的点P,设P点的横坐标为x,△PAB的铅垂高为h,则
由S△PAB=S△CAB 得:
化简得:
解得 ………………………………………………………………… 10分
将代入
中,得
![]() .
.
所以存在符合条件的P点,其坐标为 ……………………………… 12分
解析:略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
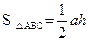 ,即三角形面积等于水平宽与铅垂高乘积的一半.
,即三角形面积等于水平宽与铅垂高乘积的一半.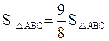 ,
,
 ,即三角形面积等于水平宽与铅垂高乘积的一半.
,即三角形面积等于水平宽与铅垂高乘积的一半. ,
,
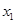 、
、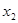 是一元二次方程
是一元二次方程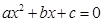 (
( ≠0)的两根,那么,
≠0)的两根,那么,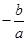 ,
,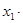
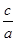 .这就是著名的韦达定理.
.这就是著名的韦达定理.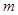 与
与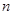 是方程
是方程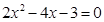 的两根,
的两根,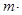
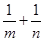 的值.
的值. ,即三角形面积等于水平宽与铅垂高乘积的一半.
,即三角形面积等于水平宽与铅垂高乘积的一半. ,
,