Question

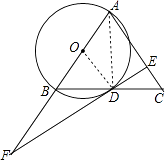
【题目】如图，在△ABC中，AB=AC，以AB为直径作⊙O交BC于点D，过点D作⊙O的切线DE交AC于点E，交AB延长线于点F．
（1）求证：DE⊥AC；
（2）若AB=10，AE=8，求BF的长．

Answer 1

【答案】
（1）证明：连接OD、AD，

∵DE切⊙O于点D，

∴OD⊥DE，

∵AB是直径，

∴∠ADB=90°，

∵AB=AC，

∴D是BC的中点，

又∵O是AB中点，

∴OD∥AC，

∴DE⊥AC

（2）解：∵AB=10，

∴OB=OD=5，

由（1）得OD∥AC，

∴△ODF∽△AEF，

∴ = = ，

设BF=x，AE=8，

∴ = ，

解得：x= ，

经检验x= 是原分式方程的根，且符合题意，

∴BF=

【解析】（1）连接OD、AD，由AB=AC且∠ADB=90°知D是BC的中点，由O是AB中点知OD∥AC，根据OD⊥DE可得；（2）证△ODF∽△AEF得 = ，据此可得答案．
【考点精析】本题主要考查了等腰三角形的性质和切线的性质定理的相关知识点，需要掌握等腰三角形的两个底角相等（简称：等边对等角）；切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题．