题目内容
在Rt△ABC中,AB=3,BC=4,∠B=9O°,AD、BE、CF是△ABC的三条内角平分线.那么,△DEF的面积等于分析:过F点作FQ⊥AC,过E点⊥作NE⊥AB,EM⊥BC,过D点作DH⊥AC.求证四边形NBME是正方形,设NE=x1,根据S四边形NBME+S△ANE+S△CEM=S△ABC,解得x1=
;设BF=x2.根据S△AFQ+2S△BFC=S△ABC,解得x2=
,同理解得,x3=
,然后利用∴S△DEF=S△ABC-S△AEF-S△BFD-S△CDE,将所得数值代入即可.
| 12 |
| 7 |
| 4 |
| 3 |
| 3 |
| 2 |
解答: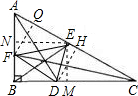 解:过F点作FQ⊥AC,过E点⊥作NE⊥AB,EM⊥BC,过D点作DH⊥AC.
解:过F点作FQ⊥AC,过E点⊥作NE⊥AB,EM⊥BC,过D点作DH⊥AC.
设NE=x1,
∵BE平分∠B,且∠B=9O°,
∴四边形NBME是正方形,
则S四边形NBME+S△ANE+S△CEM=S△ABC,
则x12+
x1(4-x1)+
x1(3-x1)=
×12,
解得,x1=
;
设BF=x2.根据CF是∠C平分线,可得△QFC≌△BFC,
则S△AFQ+2S△BFC=S△ABC,
则
x2×1+2(
x2×4)=
×12,
解得,x2=
,
则AF=AB-x2=
;
设BD=x3,
同理解得,x3=
,
则CD=4-
=
,
∴S△DEF=S△ABC-S△AEF-S△BFD-S△CDE
=
AB•BC-
AF•NE-
BF•FD-
CD•EM
=6-
(
×
)-
(
×
)-
(
×
)
=
.
故答案为:
.
 解:过F点作FQ⊥AC,过E点⊥作NE⊥AB,EM⊥BC,过D点作DH⊥AC.
解:过F点作FQ⊥AC,过E点⊥作NE⊥AB,EM⊥BC,过D点作DH⊥AC.设NE=x1,
∵BE平分∠B,且∠B=9O°,
∴四边形NBME是正方形,
则S四边形NBME+S△ANE+S△CEM=S△ABC,
则x12+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得,x1=
| 12 |
| 7 |
设BF=x2.根据CF是∠C平分线,可得△QFC≌△BFC,
则S△AFQ+2S△BFC=S△ABC,
则
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得,x2=
| 4 |
| 3 |
则AF=AB-x2=
| 5 |
| 3 |
设BD=x3,
同理解得,x3=
| 3 |
| 2 |
则CD=4-
| 3 |
| 2 |
| 5 |
| 2 |
∴S△DEF=S△ABC-S△AEF-S△BFD-S△CDE
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=6-
| 1 |
| 2 |
| 5 |
| 3 |
| 12 |
| 7 |
| 1 |
| 2 |
| 4 |
| 3 |
| 3 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 12 |
| 7 |
=
| 10 |
| 7 |
故答案为:
| 10 |
| 7 |
点评:本题主要考查学生对角平分线的性质,全等三角形的判定与性质,正方形的判定与性质等知识点的灵活运用,此题涉及到的知识点较多,需要做多条辅助线,计算步骤繁琐,要特别仔细认真,稍有疏忽就出错,属于难题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
在Rt△ABC中,已知a及∠A,则斜边应为( )
| A、asinA | ||
B、
| ||
| C、acosA | ||
D、
|
 如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )
如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )| A、9:4 | B、9:2 | C、3:4 | D、3:2 |
 已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径.
已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径. 如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )
如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )