��Ŀ����
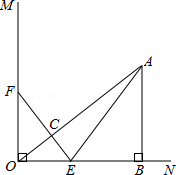
��ͼ����֪��MON=90�㣬A�ǡ�MON�ڲ���һ�㣬����A��AB��ON������Ϊ��B��AB=3���ף�OB=4���ף�����E��Fͬʱ��O���������E��1.5����/����ٶ���ON�����˶�����F��2����/����ٶ���OM�����˶���EF��OA���ڵ�C������AE������E�����Bʱ����F��ֹ֮ͣ�˶������˶�ʱ��Ϊt�루t��0����
��1����t=1��ʱ����EOF���ABO�Ƿ����ƣ���˵�����ɣ�
��2�����˶������У�����tȡ��ֵʱ������EF��OA��Ϊʲô��
��3������AF�����˶������У��Ƿ����ijһʱ��t��ʹ��S��AEF= S�ı���ABOF�������ڣ��������ʱt��ֵ���������ڣ���˵�����ɣ�
S�ı���ABOF�������ڣ��������ʱt��ֵ���������ڣ���˵�����ɣ�
��1����t=1��ʱ����EOF���ABO�Ƿ����ƣ���˵�����ɣ�
��2�����˶������У�����tȡ��ֵʱ������EF��OA��Ϊʲô��
��3������AF�����˶������У��Ƿ����ijһʱ��t��ʹ��S��AEF=
 S�ı���ABOF�������ڣ��������ʱt��ֵ���������ڣ���˵�����ɣ�
S�ı���ABOF�������ڣ��������ʱt��ֵ���������ڣ���˵�����ɣ�
��1����EOF�ס�ABO�����ɼ�����
��2�����ɼ�����
��3�����ڣ���t= ��t=
��t= ʱ��S��AEF=
ʱ��S��AEF= S�ı���ABOF��
S�ı���ABOF��
��2�����ɼ�����
��3�����ڣ���t=
 ��t=
��t= ʱ��S��AEF=
ʱ��S��AEF= S�ı���ABOF��
S�ı���ABOF�������������1����
 =
= ����MON=��ABE=90�㣬�ɵó���EOF�ס�ABO��
����MON=��ABE=90�㣬�ɵó���EOF�ס�ABO����2��֤��Rt��EOF��Rt��ABO������֤��EF��OA��
��3������֪S��AEF=
 S�ı���ABOF���ó�S��FOE+S��ABE=
S�ı���ABOF���ó�S��FOE+S��ABE= S����ABOF���Ӷ������t��ֵ��
S����ABOF���Ӷ������t��ֵ�������������1����t=1��
��OE=1.5���ף�OF=2���ף�
��AB=3���ף�OB=4���ף�
��
 ��
��
�ߡ�MON=��ABE=90�㣬
���EOF�ס�ABO��
��2�����˶������У�OE=1.5t��OF=2t��
��AB=3��OB=4��
��
 ��
���֡ߡ�EOF=��ABO=90�㣬
��Rt��EOF��Rt��ABO��
���AOB=��EOF��
�ߡ�AOB+��FOC=90�㣬
���EOF+��FOC=90�㣬
��EF��OA��
��3����ͼ������AF��

��OE=1.5t��OF=2t��
��BE=4��1.5t
��S��FOE=
 OE•OF=
OE•OF= ��1.5t��2t=
��1.5t��2t= t2��S��ABE=
t2��S��ABE= ����4��1.5t����3=6��
����4��1.5t����3=6�� t��
t��S����ABOF=
 ��2t+3����4=4t+6
��2t+3����4=4t+6��S��AEF=
 S�ı���ABOF
S�ı���ABOF��S��FOE+S��ABE=
 S����ABOF��
S����ABOF����
 t2+6��
t2+6�� t=
t= ��4t+6������6t2��17t+12=0��
��4t+6������6t2��17t+12=0�����t=
 ��t=
��t= ��
���൱t=
 ��t=
��t= ʱ��S��AEF=
ʱ��S��AEF= S�ı���ABOF��
S�ı���ABOF��
��ϰ��ϵ�д�
 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д� ������ĩ��ϰ��ѵ��ϵ�д�
������ĩ��ϰ��ѵ��ϵ�д�
�����Ŀ




 ��BC=4������BD����BAD��ƽ���߽�BD�ڵ�E����AE��CD
��BC=4������BD����BAD��ƽ���߽�BD�ڵ�E����AE��CD







