题目内容
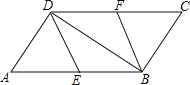
【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.
(1)求证:△ADE≌△CBF ;
(2)当AD⊥BD时,请你判断四边形BFDE的形状,并说明理由.
【答案】(1)证明见解析;(2)菱形.
【解析】试题分析: (1)根据平行四边形的性质可得∠A=∠C,AD=BC,CD=AB,进而可得CF=AE,然后利用SAS定理判定△ADE≌△CBF;
(2)首先证明四边形ABCD是平行四边形,再根据直角三角形的性质可得DE=EB,根据邻边相等的平行四边形是菱形可得结论.
试题解析:
(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=BC,CD=AB,
∵E、F分别为边AB、CD的中点,
∴CF=AE,
在△ADE和△CBF中,
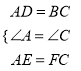 ,
,
∴△ADE≌△CBF(SAS);
(2)菱形,
∵△ADE≌△CBF,
∴ED=BF,
∵DF=EB,
∴四边形ABCD是平行四边形,
∵AD⊥BD,E为边AB中点,
∴DE=![]() AB,
AB,
∴DE=EB,
∴四边形BFDE是菱形.
点睛: 此题主要考查了菱形的判定,以及平行四边形的性质,全等三角形的判定与性质,关键是掌握邻边相等的平行四边形是菱形.

练习册系列答案
相关题目