题目内容
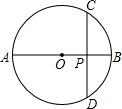 (2013•潍坊)如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP:AP=1:5,则CD的长为( )
(2013•潍坊)如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP:AP=1:5,则CD的长为( )分析:先根据⊙O的直径AB=12求出OB的长,再由BP:AP=1:5求出BP的长,故可得出OP的长,连接OC,在Rt△OPC中利用勾股定理可求出PC的长,再根据垂径定理即可得出结论.
解答: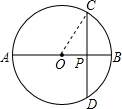 解:∵⊙O的直径AB=12,
解:∵⊙O的直径AB=12,
∴OB=
AB=6,
∵BP:AP=1:5,
∴BP=
AB=
×12=2,
∴OP=OB-BP=6-2=4,
∵CD⊥AB,
∴CD=2PC.
如图,连接OC,在Rt△OPC中,
∵OC=6,OP=4,
∴PC=
=
=2
,
∴CD=2PC=2×2
=4
.
故选D.
 解:∵⊙O的直径AB=12,
解:∵⊙O的直径AB=12,∴OB=
| 1 |
| 2 |
∵BP:AP=1:5,
∴BP=
| 1 |
| 6 |
| 1 |
| 6 |
∴OP=OB-BP=6-2=4,
∵CD⊥AB,
∴CD=2PC.
如图,连接OC,在Rt△OPC中,
∵OC=6,OP=4,
∴PC=
| OC2-OP2 |
| 62-42 |
| 5 |
∴CD=2PC=2×2
| 5 |
| 5 |
故选D.
点评:本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
 (2013•潍坊)如图是常用的一种圆顶螺杆,它的俯视图正确的是( )
(2013•潍坊)如图是常用的一种圆顶螺杆,它的俯视图正确的是( )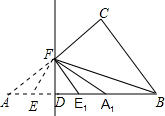 (2013•潍坊)如图,直角三角形ABC中,∠ACB=90°,AB=10,BC=6,在线段AB上取一点D,作DF⊥AB交AC于点F,现将△ADF沿DF折叠,使点A落在线段DB上,对应点记为A1;AD的中点E的对应点记为E1,若△E1FA1∽△E1BF,则AD=
(2013•潍坊)如图,直角三角形ABC中,∠ACB=90°,AB=10,BC=6,在线段AB上取一点D,作DF⊥AB交AC于点F,现将△ADF沿DF折叠,使点A落在线段DB上,对应点记为A1;AD的中点E的对应点记为E1,若△E1FA1∽△E1BF,则AD=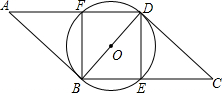 (2013•潍坊)如图,四边形ABCD是平行四边形,以对角线BD为直径作⊙O,分别与BC,AD相交于点E,F.
(2013•潍坊)如图,四边形ABCD是平行四边形,以对角线BD为直径作⊙O,分别与BC,AD相交于点E,F.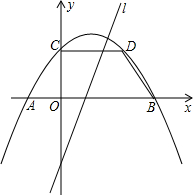 (2013•潍坊)如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交与A,B,C三点,且AB=4,点D(2,
(2013•潍坊)如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交与A,B,C三点,且AB=4,点D(2,