题目内容
如图,P是正方形ABCD内一点,在正方形ABCD外有一点E,满足∠ABE=∠CBP,BE=BP.(1)在图中是否存在两个全等的三角形,若存在请写出这两个三角形并证明;若不存在请说明理由;
(2)若(1)中存在,这两个三角形通过旋转能够互相重合吗?若重合请说出旋转的过程;若不重合请说明理由;
(3)PB与BE有怎样的位置关系,说明理由;
(4)若PA=1,PB=2,∠APB=135°,求AE的值.
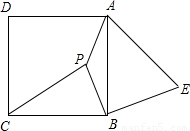
【答案】分析:(1)由AB=CB,∠ABE=∠CBP,BE=BP,可证:△CPB≌△AEB,故在图中存在两个全等的三角形;
(2)△CPB绕B点按顺时针方向旋转90°可得到△AEB,故这两个三角形通过旋转能够互相重合;
(3)由∠ABE=∠CBP,∠CBP+∠ABP=90°,可得:∠ABP+∠ABE=90°,故PB⊥BE;
(4)在Rt△PBE中,BE=BP,可得:∠BPE=45°,PE=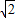 PB;又∠APB=135°可得:∠APE=90°,故在Rt△APB中,运用勾股定理可将AE的长求出.
PB;又∠APB=135°可得:∠APE=90°,故在Rt△APB中,运用勾股定理可将AE的长求出.
解答: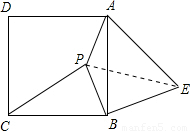 解:(1)存在,△CPB≌△AEB.
解:(1)存在,△CPB≌△AEB.
证明:∵四边形ABCD是正方形,
∴AB=CB,
∵∠ABE=∠CBP,BE=BP,
∴△CPB≌△AEB;
(2)能重合.△CPB绕B点按顺时针方向旋转90°可得到△AEB;
(3)PB⊥BE.
理由如下:由(1)知:△CPB≌△AEB,
∴∠ABE=∠CBP,
∵四边形ACBD是正方形,
∴∠ABC=90°即∠CBP+∠ABP=90°,
∴∠ABE+∠ABP=90°,
∴PB⊥BE;
(4)连接PE,
∵PB=EB,
∴∠BPE=∠BEP,
∵∠PBE=90°,
∴∠BPE=45°,
∵∠APB=135°,
∴∠APE=∠APB-∠BPE=90°,
在Rt△BPE中,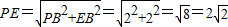 ,
,
在Rt△APE中,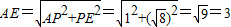 .
.
点评:本题主要考查全等三角形的判定定理及勾股定理在解直角三角形中的应用.
(2)△CPB绕B点按顺时针方向旋转90°可得到△AEB,故这两个三角形通过旋转能够互相重合;
(3)由∠ABE=∠CBP,∠CBP+∠ABP=90°,可得:∠ABP+∠ABE=90°,故PB⊥BE;
(4)在Rt△PBE中,BE=BP,可得:∠BPE=45°,PE=
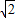 PB;又∠APB=135°可得:∠APE=90°,故在Rt△APB中,运用勾股定理可将AE的长求出.
PB;又∠APB=135°可得:∠APE=90°,故在Rt△APB中,运用勾股定理可将AE的长求出.解答:
 解:(1)存在,△CPB≌△AEB.
解:(1)存在,△CPB≌△AEB.证明:∵四边形ABCD是正方形,
∴AB=CB,
∵∠ABE=∠CBP,BE=BP,
∴△CPB≌△AEB;
(2)能重合.△CPB绕B点按顺时针方向旋转90°可得到△AEB;
(3)PB⊥BE.
理由如下:由(1)知:△CPB≌△AEB,
∴∠ABE=∠CBP,
∵四边形ACBD是正方形,
∴∠ABC=90°即∠CBP+∠ABP=90°,
∴∠ABE+∠ABP=90°,
∴PB⊥BE;
(4)连接PE,
∵PB=EB,
∴∠BPE=∠BEP,
∵∠PBE=90°,
∴∠BPE=45°,
∵∠APB=135°,
∴∠APE=∠APB-∠BPE=90°,
在Rt△BPE中,
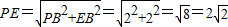 ,
,在Rt△APE中,
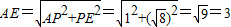 .
.点评:本题主要考查全等三角形的判定定理及勾股定理在解直角三角形中的应用.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 如图,E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,F、G是垂足,若正方形ABCD周长为a,则EF+EG等于( )
如图,E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,F、G是垂足,若正方形ABCD周长为a,则EF+EG等于( )A、
| ||
B、
| ||
| C、a | ||
| D、2a |

 22、如图,ABCD是正方形,P是对角线BD上一点,过P点作直线EF、GH分别平行于AB、BC,交两组对边于E、F、G、H,则四边形PEDG,四边形PHBF都是正方形,四边形PEAH、四边形PGCF都是矩形,设正方形PEDG的边长是a,正方形PHBF的边长是b. 请动手实践并得出结论:
22、如图,ABCD是正方形,P是对角线BD上一点,过P点作直线EF、GH分别平行于AB、BC,交两组对边于E、F、G、H,则四边形PEDG,四边形PHBF都是正方形,四边形PEAH、四边形PGCF都是矩形,设正方形PEDG的边长是a,正方形PHBF的边长是b. 请动手实践并得出结论: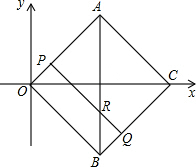 ,两点运动到相遇停止.设△OPQ的面积为S.请求出S关于t的函数关系式以及自变量t的取值范围.
,两点运动到相遇停止.设△OPQ的面积为S.请求出S关于t的函数关系式以及自变量t的取值范围.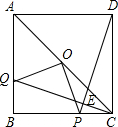 点P,连接OP,OQ;
点P,连接OP,OQ;