题目内容
【题目】已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC、DC(或它们的延长线)于点M,N.

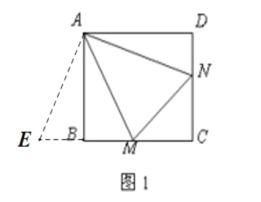
(1)当∠MAN绕点A旋转到(如图1)时,求证:BM+DN=MN;
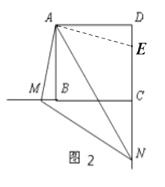
(2)当∠MAN绕点A旋转到如图2的位置时,猜想线段BM,DN和MN之间又有怎样的数量关系呢?请直接写出你的猜想。(不需要证明)
【答案】(1)见解析;(2)DN-BM=MN
【解析】
(1)根据题意延长CB至E使得BE=DN,连接AE,利用全等三角形判定证明△ABE≌△AND和△EAM≌△NAM,等量代换即可求证BM+DN=MN;
(2)由题意在DN上截取DE=MB,连接AE,证△ABM≌△ADE,推出AM=AE;∠MAB=∠EAD,求出∠EAN=∠MAN,根据SAS证△AMN≌△AEN,推出MN=EN即可.
解:(1)证明:如图1,延长CB至E使得BE=DN,连接AE,
∵四边形ABCD是正方形,
∴AB=AD,∠D=∠ABC=90°=∠ABE,
在△ADN和△ABE中
∵AD=AB∠D=∠ABEDN=BE,
△ABE≌△ADN(SAS),
∴∠BAE=∠DAN,AE=AN,
∴∠EAN=∠BAE+∠BAN=∠DAN+∠BAN=90°,
∵∠MAN=45°,
∴∠EAM=∠MAN,
∵在△EAM和△NAM中
AE=AN∠EAM=∠NAMAM=AM,
∴△EAM≌△NAM,
∴MN=ME,
∵ME=BM+BE=BM+DN,
∴BM+DN=MN;
(2)猜想:线段BM,DN和MN之间的等量关系为:DN-BM=MN.
证明:如图2,在DN上截取DE=MB,连接AE,
∵AD=AB,∠D=∠ABM=90°,BM=DE,
∴△ABM≌△ADE(SAS).
∴AM=AE;∠MAB=∠EAD,
∵∠MAN=45°=∠MAB+∠BAN,
∴∠DAE+∠BAN=45°,
∴∠EAN=90°-45°=45°=∠MAN,
∵在△AMN和△AEN中,AM=AE,∠MAN=∠EAN,AN=AN,
∴△AMN≌△AEN(SAS),
∴MN=EN,
∵DN-DE=EN,
∴DN-BM=MN.