题目内容
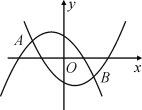
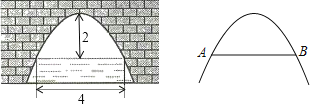
【题目】如图是一个横断面为抛物线形状的拱桥,当水面宽(AB)为4m时,拱顶(拱桥洞的最高点)离水面2m.当水面下降1m时,求水面的宽度增加了多少?
【答案】水面宽度增加了(2![]() ﹣4)米
﹣4)米
【解析】
根据已知建立直角坐标系,进而求出二次函数解析式,再通过把y=-1代入抛物线解析式得出水面宽度,即可得出答案.
解:建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,
抛物线以y轴为对称轴,且经过A,B两点,OA和OB可求出为AB的一半2米,抛物线顶点C坐标为(0,2),
设顶点式y=ax2+2,代入A点坐标(﹣2,0),
得出:a=﹣0.5,
所以抛物线解析式为y=﹣0.5x2+2,
当水面下降1米,通过抛物线在图上的观察可转化为:
当y=﹣1时,对应的抛物线上两点之间的距离,也就是直线y=﹣1与抛物线相交的两点之间的距离,
可以通过把y=﹣1代入抛物线解析式得出:
﹣1=﹣0.5x2+2,
解得:x=±![]() ,
,
所以水面宽度增加了(2![]() ﹣4)米.
﹣4)米.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案【题目】为迎接“世界华人炎帝故里寻根节”,某工厂接到一批纪念品生产订单,按要求在15天内完成,约定这批纪念品的出厂价为每件20元,设第x天(1≤x≤15,且x为整数)每件产品的成本是p元,p与x之间符合一次函数关系,部分数据如表:
天数(x) | 1 | 3 | 6 | 10 |
每件成本p(元) | 7.5 | 8.5 | 10 | 12 |
任务完成后,统计发现工人李师傅第x天生产的产品件数y(件)与x(天)满足如下关系:y=![]() ,
,
设李师傅第x天创造的产品利润为W元.
(1)直接写出p与x,W与x之间的函数关系式,并注明自变量x的取值范围:
(2)求李师傅第几天创造的利润最大?最大利润是多少元?
(3)任务完成后.统计发现平均每个工人每天创造的利润为299元.工厂制定如下奖励制度:如果一个工人某天创造的利润超过该平均值,则该工人当天可获得20元奖金.请计算李师傅共可获得多少元奖金?
【题目】为了解学生每天的睡眠情况,某初中学校从全校 800 名学生中随机抽取了 40 名学生,调查了他们平均每天的睡眠时间(单位: h) ,统计结果如下:
9,8,10.5,7,9,8,10,9.5,8,9,9.5,7.5,9.5,9,8.5,7.5,10,9.5,8,9,
7,9.5,8.5,9,7,9,9,7.5,8.5,8.5,9,8,7.5,9.5,10,9.5,8.5,9,8,9.
在对这些数据整理后,绘制了如下的统计图表:
睡眠时间分组统计表 睡眠时间分布情况
组别 | 睡眠时间分组 | 人数(频数) |
1 | 7≤t<8 | m |
2 | 8≤t<9 | 11 |
3 | 9≤t<10 | n |
4 | 10≤t<11 | 4 |

请根据以上信息,解答下列问题:
(1) m = , n = , a = , b = ;
(2)抽取的这 40 名学生平均每天睡眠时间的中位数落在 组(填组别) ;
(3)如果按照学校要求,学生平均每天的睡眠时间应不少于 9 h,请估计该校学生中睡眠时间符合要求的人数.