Question

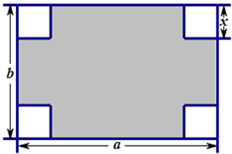如图所示，在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形．
（1）用a，b，x表示纸片剩余部分的面积；
（2）当a=6，b=4，且剪去部分的面积等于剩余部分的面积时，求正方形的边长．

Answer 1

分析：（1）边长为x的正方形面积为x²，矩形面积减去4个小正方形的面积即可．
（2）依据剪去部分的面积等于剩余部分的面积，列方程求出x的值即可．

解答：解：（1）ab-4x²；（2分）

（2）依题意有：ab-4x²=4x²，（4分）
将a=6，b=4，代入上式，得x²=3，（6分）
解得x₁=

3

，x₂=-

3

（舍去）．（7分）
即正方形的边长为

3

点评：本题是利用方程解答几何问题，充分体现了方程的应用性．
依据等量关系“剪去部分的面积等于剩余部分的面积”，建立方程求解．