题目内容
【题目】已知二次函数y=x2+(m﹣1)x+3的图象过点(2,﹣1),
(1)求此二次函数的解析式;
(2)画出这个二次函数的图象;并确定y>0时,x的取值范围?
(3)设此二次函数图象与x轴交点分别为A、B(A在B左侧)与y轴交点为C,求△ABC的面积.
【答案】(1)y=x2﹣4x+3;(2),y>0时,x的取值范围x<1或x>3;(3)3.
【解析】
(1)根据二次函数y=x2+(m-1)x+3的图象过点(2,-1),可以求得m的值,从而可以求得该函数的解析式;
(2)根据(1)中的函数解析式可以求得该函数与x轴的交点和该函数的顶点坐标,从而可以画出相应的函数图象,然后根据函数图象即可确定y>0时,x的取值范围;
(3)根据(1)中的函数解析式可以得到点A、B、C的坐标,从而可以求得△ABC的面积.
(1)∵二次函数y=x2+(m﹣1)x+3的图象过点(2,﹣1),
∴﹣1=22+(m﹣1)×2+3,
解得,m=﹣3,
∴此函数的二次函数解析式为y=x2﹣4x+3;
(2)∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴该函数的顶点坐标为(2,﹣1),
当y=0时,0=x2﹣4x+3,得x1=1,x2=3,
∴该函数与x轴的交点坐标为(1,0),(3,0),
这个二次函数的图象如图所示,
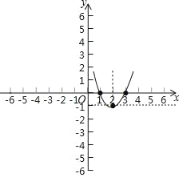
由图象可得,y>0时,x的取值范围x<1或x>3;
(3)∵此二次函数图象与x轴交点分别为A、B(A在B左侧)与y轴交点为C,
∴点A(1,0),点B(3,0),点C(0,3),
∴△ABC的面积是:![]() =3.
=3.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目