题目内容
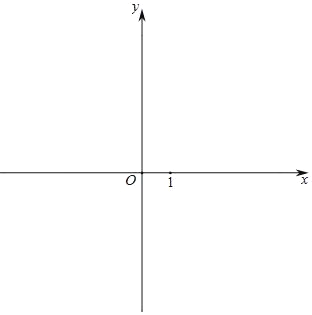
【题目】如图,矩形OABC在平面直角坐标系中,若x2﹣2![]() x+2=0的两根是x1、x2,且OC=x1+x2,OA=x1x2
x+2=0的两根是x1、x2,且OC=x1+x2,OA=x1x2
(1)求B点的坐标.
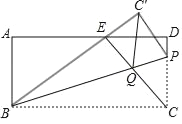
(2)把△ABC沿AC对折,点B落在点B′处,线段AB′与x轴交于点D,求直线BD的解析式.
(3)在平面上是否存在点P,使D、C、B、P四点形成的四边形为平形四边形?若存在,请直接写出P点坐标;若不存在,请说明理由.

【答案】(1)B(2![]() ,2);(2)y=
,2);(2)y=![]()
![]() x-1;(3)存在,P1(
x-1;(3)存在,P1(![]()
![]() ,2), P2(
,2), P2(![]()
![]() ,2) ,P3(
,2) ,P3(![]()
![]() ,-2).
,-2).
【解析】
(1)根据一元二次方程的两根关系求出x1+x2,x1x2,从而得到点B的坐标;
(2)根据矩形的性质,∠BAC=∠AOB=30°,然后根据全等三角形的判定得到△ABC≌△ABC,然后根据勾股定理求出OD的长,进而得到D点的坐标;
(3)根据平行四边形的特点,对边平行且相等,由平行四边形的判定得到符合条件的点的坐标.
(1)x2-2![]() x+2=0的两根是x1、x2,
x+2=0的两根是x1、x2,
x1+x2=2![]() ,x1x2=2
,x1x2=2
∵OC= x1+x2 OA= x1x2
∴OC=2![]() , OA=2
, OA=2
∴B(2![]() ,2)
,2)
(2)在矩形OABC中 BC=2 AB=2![]()
∴∠BAC =30°=∠AOB
∴△ABC≌△AB’C
∴∠B’AC =30°得到
∴∠BAO=30°
∴AD=DC
∴AD=2![]() -DO
-DO
AD2=OD2+OA2
OD=![]()
D(![]() ,0)
,0)
设直线BD的解析式为y=kx+b(k≠0,k、b为常数)
代入B(2![]() ,2) D(
,2) D(![]() ,0)得
,0)得
k=![]() ,
,
b=-1,
∴直线BD的解析式为y=![]() x-1
x-1
(3)存在,
P1(![]() ,2), P2(
,2), P2(![]() ,2) P3(
,2) P3(![]() ,-2)
,-2)

练习册系列答案
相关题目