题目内容
【题目】如图,在![]() 中,
中,![]() ,点P是
,点P是![]() 边上的动点(不与点A,B重合).把
边上的动点(不与点A,B重合).把![]() 沿过点P的直线l折叠,点B的对应点是点D,折痕为
沿过点P的直线l折叠,点B的对应点是点D,折痕为![]() .
.

(1)若点D恰好在![]() 边上.
边上.
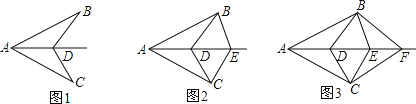
①如图1,当![]() 时,连结
时,连结![]() ,求证:
,求证:![]() .
.
②如图2,当![]() ,且
,且![]() ,
,![]() ,求
,求![]() 与
与![]() 的周长差.
的周长差.
(2)如图3,点P在![]() 边上运动时,若直线l始终垂直于
边上运动时,若直线l始终垂直于![]() ,
,![]() 的面积是否变化?请说明理由.
的面积是否变化?请说明理由.
【答案】(1)证明见解析;(2)12;(3)不变,理由见解析.
【解析】
(1)①由折叠的性质和平行线的性质可得BQ=QC,再由等腰三角形三线合一的性质即可得出结论;
②先根据勾股定理求出AP的长,再根据三角形周长的求法即可得出结论;
(2)根据折叠的性质得出DP=BP,AP=CP,再根据SAS证明△DPA≌△BPC,得出S△ACD=S△ABC,即可得出结论.
(1)①由折叠的性质可知:BQ=DQ,∠BQP=∠PQD.
∵PQ∥AC,∴∠BQP=∠C,∠PQD=∠QDC,
∴∠C=∠QDC,∴DQ=CQ,
∴BQ=QC.
∵AB=AC,∴AQ⊥BC.
②设AP=x,则AB=AC=x+3.
∵AC=AD+DC=AD+2,∴AD=x+1.
∵DP⊥AB,∴∠APD=90°,
∴![]() ,
,
∴![]() ,
,
解得:x=4.
△ABC的周长-△CDQ的周长=AB+AC+BC-(DC+CQ+DQ)
=AB+AC+BC-(DC+CQ+BQ)
=AB+AC+BC-(DC+BC)
=AB+AC-DC
=2AB-DC
=2(x+3)-2
=2x+4
=2×4+4
=12.
(2)S△ACD不会发生变化.理由如下:
连接BD,
∵B是关于直线l的对称点,
∴![]() ,
,
∴![]()
∵S△ACD=S△ABC是固定不变的,
∴S△ACD不会发生变化.


练习册系列答案
相关题目