题目内容
阅读下面的情景对话,然后解答问题:
老师:我们新定义一种三角形,两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.
小华:等边三角形一定是奇异三角形!
小明:那直角三角形是否存在奇异三角形呢?
(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”这句话是对还是错?
(2)在Rt△ABC中,两边长分别是a=5
、c=10,这个三角形是否是奇异三角形?请说明理由.
(3)在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求(b+c):a的值.
老师:我们新定义一种三角形,两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.
小华:等边三角形一定是奇异三角形!
小明:那直角三角形是否存在奇异三角形呢?
(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”这句话是对还是错?
对
对
(2)在Rt△ABC中,两边长分别是a=5
| 2 |
(3)在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求(b+c):a的值.
分析:(1)根据题中所给的奇异三角形的定义直接进行判断即可;
(2)分c是斜边和b是斜边两种情况,再根据勾股定理判断出所给的三角形是否符合奇异三角形的定义;
(3)先根据勾股定理得出Rt△ABC各边之间的关系,再根据此三角形是奇异三角形可用a表示出b、c的值,代入(b+c):a进行计算.
(2)分c是斜边和b是斜边两种情况,再根据勾股定理判断出所给的三角形是否符合奇异三角形的定义;
(3)先根据勾股定理得出Rt△ABC各边之间的关系,再根据此三角形是奇异三角形可用a表示出b、c的值,代入(b+c):a进行计算.
解答:解:(1)对 (填对或错)(2分)
(2)①当c为斜边时,b=
=5
∴a=b
∴a2+c2≠2b2(或b2+c2≠2a2),
∴Rt△ABC不是奇异三角形.
②当b为斜边时,b=
=5
,
∵a2+b2=200
∴2c2=200
∴a2+b2=2c2
∴Rt△ABC是奇异三角形. (2分)
(3)(6分)
在Rt△ABC中,a2+b2=c2,
∵c>b>a>0
∴2c2>a2+b2,2a2<b2+c2,
∵Rt△ABC是奇异三角形,
∴a2+c2=2b2(3分)
∴2b2=a2+(a2+b2),
∴b2=2a2得b=
a
∵c2=a2+b2=3a2,
∴c=
a
∴(b+c):a=(
a+
a):a=
+
.
(2)①当c为斜边时,b=
| c2-a2 |
| 2 |
∴a=b
∴a2+c2≠2b2(或b2+c2≠2a2),
∴Rt△ABC不是奇异三角形.
②当b为斜边时,b=
| c2+a2 |
| 6 |
∵a2+b2=200
∴2c2=200
∴a2+b2=2c2
∴Rt△ABC是奇异三角形. (2分)
(3)(6分)
在Rt△ABC中,a2+b2=c2,
∵c>b>a>0
∴2c2>a2+b2,2a2<b2+c2,
∵Rt△ABC是奇异三角形,
∴a2+c2=2b2(3分)
∴2b2=a2+(a2+b2),
∴b2=2a2得b=
| 2 |
∵c2=a2+b2=3a2,
∴c=
| 3 |
∴(b+c):a=(
| 2 |
| 3 |
| 2 |
| 3 |
点评:本题考查的是勾股定理的应用,在解答(2)时要注意分类讨论.

练习册系列答案
相关题目


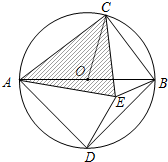

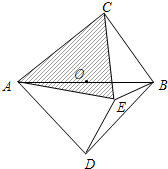 阅读下面的情景对话,然后解答问题:
阅读下面的情景对话,然后解答问题:
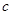 ,AC=
,AC=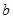 ,BC=
,BC=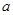 ,且
,且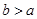 ,若Rt△ABC是奇异三角形,求
,若Rt△ABC是奇异三角形,求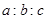 ;
; 