Question

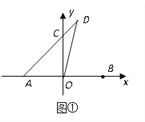
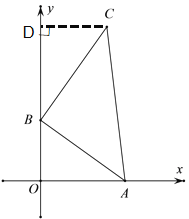
【题目】如图，在平面直角坐标系中，以A（2,0），B（0，t）为顶点作等腰直角△ABC（其中∠ABC=90°，且点C落在第一象限内），则点C关于y轴的对称点C’的坐标为___．（用t的代数式表示）

Answer 1

【答案】

【解析】

作CD⊥y轴于点D，证明△CDB与△BOA全等，求出点C的坐标，再根据关于y轴对称的点的坐标即可得解．

解：过点C作CD⊥y轴于点D，如图：

∵△ABC是等腰直角三角形，
∴BC=AB，∠ABC=90°，
∴∠CBD+∠ABO=90°，
∵∠CBD+∠BCD=90°，
∴∠ABO=∠BCD，
在△BCD与△ABO中，

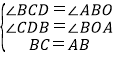
∴△BCD≌△ABO（AAS），
∴CD=BO，BD=AO，
∵A（2，0），B（0，t），
∴AO=2=BD，BO=t，CD=t
∴DO= OB + BD =t+2，
∴C点的坐标为（t，t+2）．

∵点C与点C′关于y轴的对称

∴点C′的坐标为.

故答案为：.