题目内容
【题目】如图,在等腰![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 出发沿
出发沿![]() 路径以
路径以![]() 的速度运动,设点
的速度运动,设点![]() 运动时间为
运动时间为![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 关于
关于![]() 的函数图象大致为( )
的函数图象大致为( )
A.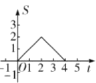 B.
B.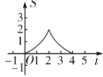 C.
C. D.
D.
【答案】A
【解析】
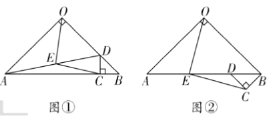
根据题意,由勾股定理求出BC的长度,当点Q运动到点A,即t=2时,![]() 的面积最大,则函数分为两段:①当点Q在AC上运动时,
的面积最大,则函数分为两段:①当点Q在AC上运动时,![]() ;②当点Q在AB上运动时,
;②当点Q在AB上运动时,![]() ;分别求出S与t的关系式,即可得到答案.
;分别求出S与t的关系式,即可得到答案.
解:在等腰![]() 中,
中,![]() ,
,
∴![]() ,
,
由等腰直角三角形的性质,当点Q运动到点A,
即t=2时,![]() 的面积最大;
的面积最大;
∵![]() ,
,
∴时间t的最大值为:![]() ;
;
①当点Q在AC上运动时,![]() ;如图,作QD⊥BC,
;如图,作QD⊥BC,
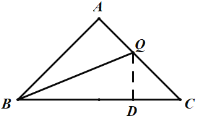
∵![]() 是等腰直角三角形,
是等腰直角三角形,
∴∠C=45°,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
②当点Q在AB上运动时,![]() ;如图,作QE⊥BC,
;如图,作QE⊥BC,

∵![]() 是等腰直角三角形,
是等腰直角三角形,
∴∠B=45°,BQ=![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
∴A选项中的图像满足S与t的关系;
故选:A.

练习册系列答案
相关题目
【题目】 “六一”前夕质监部门从某超市经销的儿童玩具、童车和童装中共抽查了300件儿童用品,以下是根据抽查结果绘制出的不完整的统计表和扇形图;
类别 | 儿童玩具 | 童车 | 童装 |
抽查件数 | 90 |

请根据上述统计表和扇形提供的信息,完成下列问题:
(1)分别补全上述统计表和统计图;
(2)已知所抽查的儿童玩具、童车、童装的合格率分别为90%、88%、80%,若从该超市的这三类儿童用品中随机购买一件,买到合格品的概率是多少?