题目内容
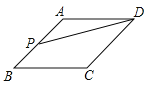
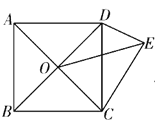
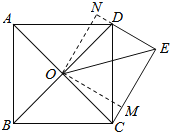
【题目】如图, ABCD 为正方形, O 为 AC 、 BD 的交点,在![]() 中,
中,![]() 90,
90, ![]() 30,若OE
30,若OE ![]() ,则正方形的面积为( )
,则正方形的面积为( )
A. 5B. 4C. 3D. 2
【答案】B
【解析】
过点O作OM⊥CE于M,作ON⊥DE交ED的延长线于N,判断出四边形OMEN是矩形,根据矩形的性质可得∠MON=90°,再求出∠COM=∠DON,根据正方形的性质可得OC=OD,然后利用“角角边”证明△COM和△DON全等,根据全等三角形对应边相等可得OM=ON,然后判断出四边形OMEN是正方形,设正方形ABCD的边长为![]() ,根据直角三角形30°角所对的直角边等于斜边的一半可得DE=
,根据直角三角形30°角所对的直角边等于斜边的一半可得DE=![]() CD,再利用勾股定理列式求出CE,根据正方形的性质求出OC=OD=
CD,再利用勾股定理列式求出CE,根据正方形的性质求出OC=OD=![]() a,然后利用四边形OCED的面积列出方程求出
a,然后利用四边形OCED的面积列出方程求出![]() ,再根据正方形的面积公式列式计算即可得解.
,再根据正方形的面积公式列式计算即可得解.
解:如图,过点O作OM⊥CE于M,作ON⊥DE交ED的延长线于N,
∵∠CED=90°,
∴四边形OMEN是矩形,
∴∠MON=90°,
∵∠COM+∠DOM=∠DON+∠DOM,
∴∠COM=∠DON,
∵四边形ABCD是正方形,
∴OC=OD,
在△COM和△DON中,
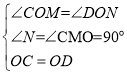 ,
,
∴△COM≌△DON(AAS),
∴OM=ON,
∴四边形OMEN是正方形,
设正方形ABCD的边长为![]() ,则OC=OD=
,则OC=OD=![]()
∵∠CED=90°,∠DCE=30°,
∴DE=![]() CD=
CD=![]() ,
,
由勾股定理得,CE=![]() ,
,
∴四边形OCED的面积=![]() ,
,
解得![]() ,
,
所以,正方形ABCD的面积=![]() .
.
故选:B.

 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案【题目】)6月5日是世界环境日,某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级的一班和二班的成绩整理并绘制成如下统计图:
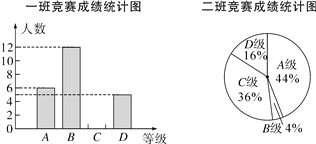
根据以上提供的信息解答下列问题:
(1)把一班竞赛成绩统计图补充完整;
(2)写出下表中a,b,c的值:
平均数(分) | 中位数(分) | 众数(分) | |
一班 | a | b | 90 |
二班 | 87.6 | 80 | c |
(3)请从以下给出的三个方面对这次竞赛成绩的结果进行分析:
①从平均数和中位数方面比较一班和二班的成绩;
②从平均数和众数方面比较一班和二班的成绩;
③从B级以上(包括B级)的人数方面来比较一班和二班的成绩.