��Ŀ����
�Ķ���
��p��q��mΪ�����������η���x3+px2+qx+m=0��������c����c���뷽�̵ã�c3+pc2+qc+m=0������ã�m=-c3-pc2-qc�����У�m=c����-c2-pc-q��������-c2-pc-q��c��m��������������c��m����������������˵��������ϵ������x3+px2+qx+m=0��������ֻ������m�����������磺����x3+4x2+3x-2=0��-2������Ϊ��1�͡�2�������Ƿֱ���뷽��x3+4x2+3x-2=0������֤�ã�x=-2�Ǹ÷��̵������⣬-1��1��2���Ƿ��̵������⣮
������⣺
��1�����������ѧϰ������ȷ������x3+x2+5x+7=0��������ֻ�������ļ���������
��2������x3-2x2-4x+3=0�Ƿ��������⣿���У�������������⣻��û�У���˵�����ɣ�
��p��q��mΪ�����������η���x3+px2+qx+m=0��������c����c���뷽�̵ã�c3+pc2+qc+m=0������ã�m=-c3-pc2-qc�����У�m=c����-c2-pc-q��������-c2-pc-q��c��m��������������c��m����������������˵��������ϵ������x3+px2+qx+m=0��������ֻ������m�����������磺����x3+4x2+3x-2=0��-2������Ϊ��1�͡�2�������Ƿֱ���뷽��x3+4x2+3x-2=0������֤�ã�x=-2�Ǹ÷��̵������⣬-1��1��2���Ƿ��̵������⣮
������⣺
��1�����������ѧϰ������ȷ������x3+x2+5x+7=0��������ֻ�������ļ���������
��2������x3-2x2-4x+3=0�Ƿ��������⣿���У�������������⣻��û�У���˵�����ɣ�
��1�����Ķ������֪���÷�������������⣬��ֻ������7����������7������ֻ�У�1��-1��7��-7���ĸ�����
��2���÷����������⣮
���̵�������ֻ������3����������1��-1��3��-3�������Ƿֱ���뷽��x3-2x2-4x+3=0
������֤�ã�x=3�Ǹ÷��̵������⣮
��2���÷����������⣮
���̵�������ֻ������3����������1��-1��3��-3�������Ƿֱ���뷽��x3-2x2-4x+3=0
������֤�ã�x=3�Ǹ÷��̵������⣮

��ϰ��ϵ�д�
�����Ŀ
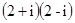 ����
����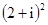 ��
�� �����a+bi����ʽ
�����a+bi����ʽ