题目内容
(2013•镇江模拟)请你设计一个包装盒,如图1所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形(E,F在AB上,是被切去的等腰直角三角形斜边的两个端点),再沿虚线折起,使得A,B,C,D四个点重合于图2中的点P,正好形成一个底为正方形的包装盒,设AE=FB=xcm.
(1)若x=20cm,包装盒底面正方形面积为
(2)设包装盒侧面积为S,
①求S与x之间的函数关系式;
②若要求包装盒侧面积S最大,问此时x应取何值?并求出最大面积;
(3)试问能否用包装盒盛放一个底面半径为15cm,高为15cm的圆柱形工艺品?若不能,说明理由;若能,求出x的值.

(1)若x=20cm,包装盒底面正方形面积为
800
800
cm2;侧面积为1600
1600
cm2(2)设包装盒侧面积为S,
①求S与x之间的函数关系式;
②若要求包装盒侧面积S最大,问此时x应取何值?并求出最大面积;
(3)试问能否用包装盒盛放一个底面半径为15cm,高为15cm的圆柱形工艺品?若不能,说明理由;若能,求出x的值.

分析:(1)由题意可以求出EF的值,就可以求出包装盒的高和地面正方形的边长,从而得出结论;
(2)①根据条件可以分别表示出阴影部分的面积,掀起的四个角上的四个等腰直角三角形的面积之和及底部正方形的面积就可以表示出S与x之间的函数关系式;
②将①的解析式化为顶点式就可以求出S的最大值;
(3)设包装盒的底面正方形的边长为a,高为h,就可以得出AE=
a,EF=60-2AE=60-
a,h=
EF=30
-a,再三种情况讨论就可以得出结论.
(2)①根据条件可以分别表示出阴影部分的面积,掀起的四个角上的四个等腰直角三角形的面积之和及底部正方形的面积就可以表示出S与x之间的函数关系式;
②将①的解析式化为顶点式就可以求出S的最大值;
(3)设包装盒的底面正方形的边长为a,高为h,就可以得出AE=
| ||
| 2 |
| 2 |
| ||
| 2 |
| 2 |
解答:解:(1)由题意,得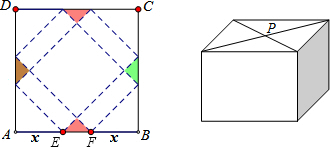
底面正方形的边长为:20
cm,
包装盒的高为:10
cm,
∴包装盒底面正方形面积为:(20
)2=800cm2;
包装盒的侧面积为:10
×20
×4=1600cm2;
故答案为:800,1600;
(2)∵AE=FB=xcm,
∴EF的长为(60-2x)cm.
图中阴影部分拼在一起是边长为EF的正方形,其面积为:(60-2x)2cm2,
掀起的四个角上的四个等腰直角三角形的面积之和为:2x2cm2;
盒底正方形的边长为
x,其面积为2x2;
∴S=602-(60-2x)2-4x2=240x-8x2
∴S=-8(x2-30x)=-8(x-15)2+1800(0<x<30),
∵a=-8<0.
∴抛物线的开口向下,S有最大值.
∴x=15cm时,侧面积最大为1800cm2,
答:若包装盒侧面积S最大=1800cm2最大,x应取15cm.
(3)包装盒的底面正方形的边长为a,高为h,
∴AE=
a,
∴EF=60-2AE=60-
a,
∴h=
EF=30
-a,
∴包装盒的高h随底面边长的增大而减小.
①圆柱的底面朝下放入,此时包装盒高h不能小于15.
∵圆柱的底面半径为15cm,
∴盒底边长最小取30cm(放入如①图),
∴h=30
-a=30(
-1)<15,故不能放下.
②圆柱体侧面朝下放入,盒高h最小取30cm,
此时底面边长最大为(30
-30)cm.
此时由两种特殊的防治方法:
若按图1放置,此时盒底边长a取30cm,
∴高为30
-30.
∵30>30
-30,
∴放不下;
若按图2放置,此时盒底边长为
a=30×
+15×
=
cm,
∵
-(30
-30)=30-
>0,
∴也不能放下.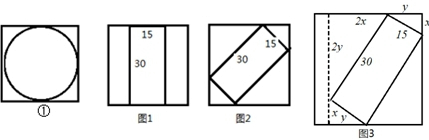
其他任意位置摆放,也不能放下,理由:
实质上就是将边长为15和30的矩形放入另一矩形,如图3,
此时矩形的面积S=(x+2y)(2x+y)=5xy+2(x2+y2),
=5x
+450=5
+450.
令x2=t(0<t<225)
∴S=5
+450.
(x=0和15为图1情况,x=
为图2情况)
∴不能位置如何摆放,正方形的边长最小只能渠道30cm,
而30>30
-30,不能放下.
综上所述,不能放下这个几何体.

底面正方形的边长为:20
| 2 |
包装盒的高为:10
| 2 |
∴包装盒底面正方形面积为:(20
| 2 |
包装盒的侧面积为:10
| 2 |
| 2 |
故答案为:800,1600;
(2)∵AE=FB=xcm,
∴EF的长为(60-2x)cm.
图中阴影部分拼在一起是边长为EF的正方形,其面积为:(60-2x)2cm2,
掀起的四个角上的四个等腰直角三角形的面积之和为:2x2cm2;
盒底正方形的边长为
| 2 |
∴S=602-(60-2x)2-4x2=240x-8x2
∴S=-8(x2-30x)=-8(x-15)2+1800(0<x<30),
∵a=-8<0.
∴抛物线的开口向下,S有最大值.
∴x=15cm时,侧面积最大为1800cm2,
答:若包装盒侧面积S最大=1800cm2最大,x应取15cm.
(3)包装盒的底面正方形的边长为a,高为h,
∴AE=
| ||
| 2 |
∴EF=60-2AE=60-
| 2 |
∴h=
| ||
| 2 |
| 2 |
∴包装盒的高h随底面边长的增大而减小.
①圆柱的底面朝下放入,此时包装盒高h不能小于15.
∵圆柱的底面半径为15cm,
∴盒底边长最小取30cm(放入如①图),
∴h=30
| 2 |
| 2 |
②圆柱体侧面朝下放入,盒高h最小取30cm,
此时底面边长最大为(30
| 2 |
此时由两种特殊的防治方法:
若按图1放置,此时盒底边长a取30cm,
∴高为30
| 2 |
∵30>30
| 2 |
∴放不下;
若按图2放置,此时盒底边长为
a=30×
| ||
| 2 |
| ||
| 2 |
45
| ||
| 2 |
∵
45
| ||
| 2 |
| 2 |
| 15 |
| 2 |
| 2 |
∴也不能放下.

其他任意位置摆放,也不能放下,理由:
实质上就是将边长为15和30的矩形放入另一矩形,如图3,
此时矩形的面积S=(x+2y)(2x+y)=5xy+2(x2+y2),
=5x
| 225-x2 |
| 225x2-x.4 |
令x2=t(0<t<225)
∴S=5
| 225t-t2 |
(x=0和15为图1情况,x=
| 15 |
| 2 |
| 2 |
∴不能位置如何摆放,正方形的边长最小只能渠道30cm,
而30>30
| 2 |
综上所述,不能放下这个几何体.
点评:本题考查了勾股定理的运用,矩形的面积的运用,正方形的性质的运用,二次函数的解析式的运用,分类讨论思想的运用,解答时分类讨论是难点.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 (2013•镇江模拟)如图,过∠CDF的一边上DC的点E作直线AB∥DF,若∠AEC=110°,则∠CDF的度数为
(2013•镇江模拟)如图,过∠CDF的一边上DC的点E作直线AB∥DF,若∠AEC=110°,则∠CDF的度数为 (2013•镇江模拟)如图,AB是⊙O的直径,圆心O到弦BC的距离是1,则AC的长是
(2013•镇江模拟)如图,AB是⊙O的直径,圆心O到弦BC的距离是1,则AC的长是