题目内容
某体育用品商店购进一批滑板,每件进价为100元,售价为130元,每星期可卖出80件.商家决定降价促销,根据市场调查,每降价5元,每星期可多卖出20件.
(1)求商家降价前每星期的销售利润为多少元?
(2)降价后,商家要使每星期的销售利润最大,应将售价定为多少元?最大销售利润是多少?
解:(1)(130-100)×80=2400(元);
∴商家降价前每星期的销售利润为2400元;
(2)设应将售价定为x元,
则销售利润y=(x-100)(80+ ×20)
×20)
=-4x2+1000x-60000=-4(x-125)2+2500.
当x=125时,y有最大值2500.
∴应将售价定为125元,最大销售利润是2500元.
分析:(1)已知原每天利润为130-100,每星期可卖出80件,则(130-100)×80=2400元.
(2)设将售价定为x元,则销售利润为y=(x-100)(80+ ×20)=-4(x-125)2+2500,故可求出y的最大值.
×20)=-4(x-125)2+2500,故可求出y的最大值.
点评:本题考查的是二次函数的应用.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.
∴商家降价前每星期的销售利润为2400元;
(2)设应将售价定为x元,
则销售利润y=(x-100)(80+
 ×20)
×20)=-4x2+1000x-60000=-4(x-125)2+2500.
当x=125时,y有最大值2500.
∴应将售价定为125元,最大销售利润是2500元.
分析:(1)已知原每天利润为130-100,每星期可卖出80件,则(130-100)×80=2400元.
(2)设将售价定为x元,则销售利润为y=(x-100)(80+
 ×20)=-4(x-125)2+2500,故可求出y的最大值.
×20)=-4(x-125)2+2500,故可求出y的最大值.点评:本题考查的是二次函数的应用.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
为了迎接市排球运动会,市排协准备新购一批排球.张会长问器材保管员:“我们现在还有多少个排球?”,保管员说:“两年前购进100个新排球,由于训练损坏,现在还有81个球.”
(1)假设这两年平均每年的损坏率相同,求损坏率.
(2)张会长说:“我们协会有奇数个训练队,如果新购进的排球,每队分得8个球,球正好都分完;如果每队分的9个球,那么有一个队分得的球不足6个,但超过2个.”那么市排协准备新购排球以及该协会有多少个训练队?
(3)张会长准备去买第(2)题中求的排球数,某体育用品商店提供如下信息:
信息一:可供选择的排球有A、B、C三种型号,但要求购买A、B型号数量相等.
信息二:如表:
设购买A、C型号排球分别为a个、b个,你能帮张会长制定一个购买方案吗?要求总费用w(元)要最省,而且要使这批排球两年后没有损坏的个数不少于27个.
(1)假设这两年平均每年的损坏率相同,求损坏率.
(2)张会长说:“我们协会有奇数个训练队,如果新购进的排球,每队分得8个球,球正好都分完;如果每队分的9个球,那么有一个队分得的球不足6个,但超过2个.”那么市排协准备新购排球以及该协会有多少个训练队?
(3)张会长准备去买第(2)题中求的排球数,某体育用品商店提供如下信息:
信息一:可供选择的排球有A、B、C三种型号,但要求购买A、B型号数量相等.
信息二:如表:
| 型号 | 每个型号批发单价(元) | 每年每个型号排球的损坏率 |
| A | 30 | 0.2 |
| B | 20 | 0.3 |
| C | 50 | 0.1 |
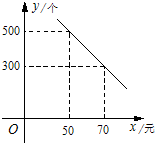 某体育用品商店购进一种品牌的篮球,每一个篮球的进价为40元,经市场调查,每月售出篮球的数量y(个)与销售单价x(元)的函数关系的图象如图所示.
某体育用品商店购进一种品牌的篮球,每一个篮球的进价为40元,经市场调查,每月售出篮球的数量y(个)与销售单价x(元)的函数关系的图象如图所示.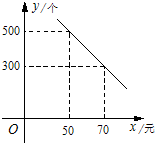 某体育用品商店购进一种品牌的篮球,每一个篮球的进价为40元,经市场调查,每月售出篮球的数量y(个)与销售单价x(元)的函数关系的图象如图所示.
某体育用品商店购进一种品牌的篮球,每一个篮球的进价为40元,经市场调查,每月售出篮球的数量y(个)与销售单价x(元)的函数关系的图象如图所示.