题目内容
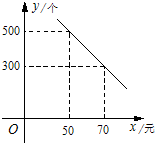 某体育用品商店购进一种品牌的篮球,每一个篮球的进价为40元,经市场调查,每月售出篮球的数量y(个)与销售单价x(元)的函数关系的图象如图所示.
某体育用品商店购进一种品牌的篮球,每一个篮球的进价为40元,经市场调查,每月售出篮球的数量y(个)与销售单价x(元)的函数关系的图象如图所示.(1)若该体育用品商店每月既能售出篮球又不亏本的条件下,请你直接写出月销售量y(个)与销售单价x(元)的函数关系式,并写出x的取值范围;
(2)8000元是否为每月销售这种篮球的最大利润?如果是,请说明理由;如果不是,请你求出月销售利润w的最大值,此时篮球的售价应定为多少元?
分析:(1)根据函数图象经过的点的坐标利用待定系数法确定一次函数的解析式即可;
(2)根据销售利润是销售量与销售一个获得利润的乘积,建立二次函数,进一步用配方法解决求最大值问题.
(2)根据销售利润是销售量与销售一个获得利润的乘积,建立二次函数,进一步用配方法解决求最大值问题.
解答:解:(1)设月销售量y(个)与销售单价x(元)的函数关系式y=kx+b,
根据图象可知直线经过点(50,500),(70,300),则
解得:
故y=-10x+1000,x的取值范围是40≤x<100.
(2)w=(x-40)(-10x+1000)
=-10x2+1400x-40000
=-10(x-70)2+9000.…(5分)
当x=70时,w取得最大值,w的最大值=9000.…(6分)
答:8000元不是每月销售这种篮球的最大利润,最大利润是9000元,此时篮球售价为70元.…(7分)
根据图象可知直线经过点(50,500),(70,300),则
|
解得:
|
故y=-10x+1000,x的取值范围是40≤x<100.
(2)w=(x-40)(-10x+1000)
=-10x2+1400x-40000
=-10(x-70)2+9000.…(5分)
当x=70时,w取得最大值,w的最大值=9000.…(6分)
答:8000元不是每月销售这种篮球的最大利润,最大利润是9000元,此时篮球售价为70元.…(7分)
点评:本题考查了二次函数的应用,利用二次函数解决实际问题,抓住基本数量关系,写出函数关系式,用配方法解决求最值问题.

练习册系列答案
相关题目
为了迎接市排球运动会,市排协准备新购一批排球.张会长问器材保管员:“我们现在还有多少个排球?”,保管员说:“两年前购进100个新排球,由于训练损坏,现在还有81个球.”
(1)假设这两年平均每年的损坏率相同,求损坏率.
(2)张会长说:“我们协会有奇数个训练队,如果新购进的排球,每队分得8个球,球正好都分完;如果每队分的9个球,那么有一个队分得的球不足6个,但超过2个.”那么市排协准备新购排球以及该协会有多少个训练队?
(3)张会长准备去买第(2)题中求的排球数,某体育用品商店提供如下信息:
信息一:可供选择的排球有A、B、C三种型号,但要求购买A、B型号数量相等.
信息二:如表:
设购买A、C型号排球分别为a个、b个,你能帮张会长制定一个购买方案吗?要求总费用w(元)要最省,而且要使这批排球两年后没有损坏的个数不少于27个.
(1)假设这两年平均每年的损坏率相同,求损坏率.
(2)张会长说:“我们协会有奇数个训练队,如果新购进的排球,每队分得8个球,球正好都分完;如果每队分的9个球,那么有一个队分得的球不足6个,但超过2个.”那么市排协准备新购排球以及该协会有多少个训练队?
(3)张会长准备去买第(2)题中求的排球数,某体育用品商店提供如下信息:
信息一:可供选择的排球有A、B、C三种型号,但要求购买A、B型号数量相等.
信息二:如表:
| 型号 | 每个型号批发单价(元) | 每年每个型号排球的损坏率 |
| A | 30 | 0.2 |
| B | 20 | 0.3 |
| C | 50 | 0.1 |
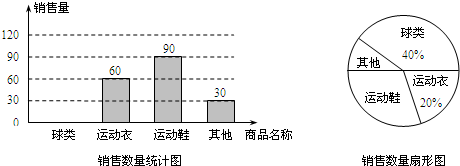
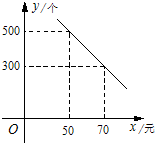 某体育用品商店购进一种品牌的篮球,每一个篮球的进价为40元,经市场调查,每月售出篮球的数量y(个)与销售单价x(元)的函数关系的图象如图所示.
某体育用品商店购进一种品牌的篮球,每一个篮球的进价为40元,经市场调查,每月售出篮球的数量y(个)与销售单价x(元)的函数关系的图象如图所示.