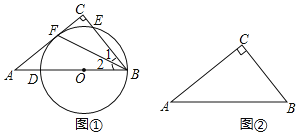
题目内容
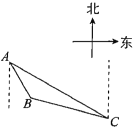
【题目】如图1:在Rt△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),试探索AD,BD,CD之间满足的等量关系,并证明你的结论.小明同学的思路是这样的:将线段AD绕点A逆时针旋转90°,得到线段AE,连接EC,DE.继续推理就可以使问题得到解决.
(1)请根据小明的思路,试探索线段AD,BD,CD之间满足的等量关系,并证明你的结论;
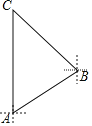
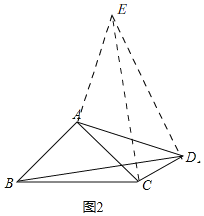
(2)如图2,在Rt△ABC中,AB=AC,D为△ABC外的一点,且∠ADC=45°,线段AD,BD,CD之间满足的等量关系又是如何的,请证明你的结论;
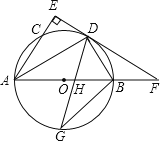
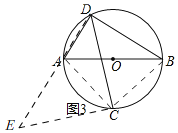
(3)如图3,已知AB是⊙O的直径,点C,D是⊙O上的点,且∠ADC=45°.
①若AD=6,BD=8,求弦CD的长为 ;
②若AD+BD=14,求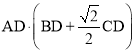 的最大值,并求出此时⊙O的半径.
的最大值,并求出此时⊙O的半径.
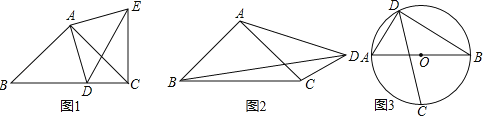
【答案】(1)CD2+BD2=2AD2,见解析;(2)BD2=CD2+2AD2,见解析;(3)①7![]() ,②最大值为
,②最大值为![]() ,半径为
,半径为![]()
【解析】
(1)先判断出∠BAD=CAE,进而得出△ABD≌△ACE,得出BD=CE,∠B=∠ACE,再根据勾股定理得出DE2=CD2+CE2=CD2+BD2,在Rt△ADE中,DE2=AD2+AE2=2AD2,即可得出结论;
(2)同(1)的方法得,ABD≌△ACE(SAS),得出BD=CE,再用勾股定理的出DE2=2AD2,CE2=CD2+DE2=CD2+2AD2,即可得出结论;
(3)先根据勾股定理的出DE2=CD2+CE2=2CD2,再判断出△ACE≌△BCD(SAS),得出AE=BD,
①将AD=6,BD=8代入DE2=2CD2中,即可得出结论;
②先求出CD=7![]() ,再将AD+BD=14,CD=7
,再将AD+BD=14,CD=7![]() 代入
代入![]() ,化简得出﹣(AD﹣
,化简得出﹣(AD﹣![]() )2+
)2+![]() ,进而求出AD,最后用勾股定理求出AB即可得出结论.
,进而求出AD,最后用勾股定理求出AB即可得出结论.
解:(1)CD2+BD2=2AD2,
理由:由旋转知,AD=AE,∠DAE=90°=∠BAC,
∴∠BAD=∠CAE,
∵AB=AC,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠B=∠ACE,
在Rt△ABC中,AB=AC,
∴∠B=∠ACB=45°,
∴∠ACE=45°,
∴∠DCE=∠ACB+∠ACE=90°,
根据勾股定理得,DE2=CD2+CE2=CD2+BD2,
在Rt△ADE中,DE2=AD2+AE2=2AD2,
∴CD2+BD2=2AD2;
(2)BD2=CD2+2AD2,
理由:如图2,
将线段AD绕点A逆时针旋转90°,得到线段AE,连接EC,DE,
同(1)的方法得,ABD≌△ACE(SAS),
∴BD=CE,在Rt△ADE中,AD=AE,
∴∠ADE=45°,
∴DE2=2AD2,
∵∠ADC=45°,
∴∠CDE=∠ADC+∠ADE=90°,
根据勾股定理得,CE2=CD2+DE2=CD2+2AD2,
即:BD2=CD2+2AD2;
(3)如图3,过点C作CE⊥CD交DA的延长线于E,
∴∠DCE=90°,
∵∠ADC=45°,
∴∠E=90°﹣∠ADC=45°=∠ADC,
∴CD=CE,
根据勾股定理得,DE2=CD2+CE2=2CD2,
连接AC,BC,
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
∵∠ADC=45°,
∴∠BDC=45°=∠ADC,
∴AC=BC,
∵∠DCE=∠ACB=90°,
∴∠ACE=∠BCD,
∴△ACE≌△BCD(SAS),
∴AE=BD,
①AD=6,BD=8,
∴DE=AD+AE=AD+BD=14,
∴2CD2=142,
∴CD=7![]() ,
,
故答案为7![]() ;
;
②∵AD+BD=14,
∴CD=7![]() ,
,
∴![]() =AD(BD+
=AD(BD+![]() ×7
×7![]() )=AD(BD+7)
)=AD(BD+7)
=ADBD+7AD=AD(14﹣AD)+7AD=﹣AD2+21AD=﹣(AD﹣![]() )2+
)2+![]() ,
,
∴当AD=![]() 时,
时,![]() 的最大值为
的最大值为![]() ,
,
∵AD+BD=14,
∴BD=14﹣![]() =
=![]() ,
,
在Rt△ABD中,根据勾股定理得,AB=![]() ,
,
∴⊙O的半径为OA=![]() AB=
AB=![]() .
.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案