题目内容
如图,河流的两岸PQ、MN互相平行,河岸MN上有一排间隔为50米的电线杆C、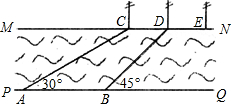 D、E、…,某人在河岸PQ的A处测得∠DBQ=45°,求河流的宽度(结果精确到0.1米).参考值:
D、E、…,某人在河岸PQ的A处测得∠DBQ=45°,求河流的宽度(结果精确到0.1米).参考值:
=1.414;
=1.732.
 D、E、…,某人在河岸PQ的A处测得∠DBQ=45°,求河流的宽度(结果精确到0.1米).参考值:
D、E、…,某人在河岸PQ的A处测得∠DBQ=45°,求河流的宽度(结果精确到0.1米).参考值:| 2 |
| 3 |
分析:应合理应用∠CAQ的度数,CD的长度,所以过点D作CA的平行线得到平行四边形.过点D向对边引垂线,得到直角三角形,进而利用三角函数值求得河宽.
解答:解:过D作DH∥CA交PQ于H,过D作DG⊥PQ,垂足为G,(4分)
∵PQ∥MN,DH∥CA
∴四边形CAHD是平行四边形.
∴AH=CD=50,∠DHQ=∠CAQ=30°(5分)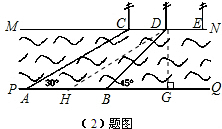
在Rt△DBG中,∵∠DBG=∠BDG=45°,
∴BG=DG,设BG=DG=x,
在Rt△DHG中,得HG=
x,(6分)
又BH=AB-AH=110-50=60,
∴60+x=
x,
∴x=30
+30≈82.0(米).
答:河流的宽为82.0米.(7分)
∵PQ∥MN,DH∥CA
∴四边形CAHD是平行四边形.
∴AH=CD=50,∠DHQ=∠CAQ=30°(5分)

在Rt△DBG中,∵∠DBG=∠BDG=45°,
∴BG=DG,设BG=DG=x,
在Rt△DHG中,得HG=
| 3 |
又BH=AB-AH=110-50=60,
∴60+x=
| 3 |
∴x=30
| 3 |
答:河流的宽为82.0米.(7分)
点评:本题考查解直角三角形的应用.难点是作出辅助线,利用三角函数求解.

练习册系列答案
相关题目
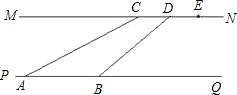 如图,河流的两岸PQ、MN互相平行,河岸MN上有一排间隔为50米的电线杆C、D、E…,某人在河岸PQ的A处测得∠CAQ=30°,然后沿河岸走了110米到达B处,测得∠DBQ=45°,求河流的宽度.
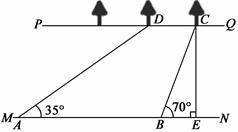
如图,河流的两岸PQ、MN互相平行,河岸MN上有一排间隔为50米的电线杆C、D、E…,某人在河岸PQ的A处测得∠CAQ=30°,然后沿河岸走了110米到达B处,测得∠DBQ=45°,求河流的宽度.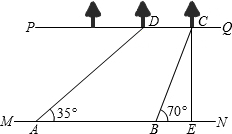 如图,河流的两岸PQ、MN互相平行,河岸PQ上有一排小树,已知相邻两树之间的距离CD=50米,某人在河岸MN的A处测得∠DAN=35°,然后沿河岸走了120米到达B处,测得∠CBN=70°.求河流的宽度CE(结果保留两个有效数字).
如图,河流的两岸PQ、MN互相平行,河岸PQ上有一排小树,已知相邻两树之间的距离CD=50米,某人在河岸MN的A处测得∠DAN=35°,然后沿河岸走了120米到达B处,测得∠CBN=70°.求河流的宽度CE(结果保留两个有效数字).