题目内容
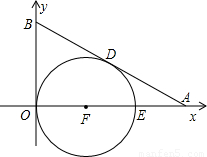
(2004•岳阳)Rt△AOB中直角边OA、OB分别在x轴、y轴的正半轴上,O为坐标原点,以F为圆心的圆与y轴、直线AB分别相切于O、D(如图),若AD=2,AE=1.(1)求BD的长度;
(2)求经过A、B两点的直线的解析式;
(3)求经过E、D、O三点的二次函数的解析式;
(4)判断(3)中抛物线的顶点是否在直线AB上.
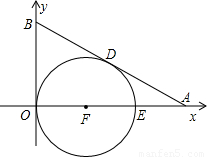
【答案】分析:(1)根据圆的切线的性质,连接DF,可得直角三角形,借助于方程,利用勾股定理求得圆的半径,利用相似求得BD的长;
(2)根据(1)的结论可得A,B的坐标,利用待定系数法可求得经过A、B两点的直线的解析式;
(3)首先求得点D的坐标,将点O,E,D的坐标代入二次函数的一般式,解方程组即可;
(4)求得抛物线的顶点坐标,再代入解析式,看是否左右相等即可.
解答: 解:(1)设⊙F的半径为r
解:(1)设⊙F的半径为r
连接DF,∴BA⊥DF
∵AD切⊙F于D点
∴AD2=AE•AO即22=1•(2r+1)
∴r= 又Rt△ADF∽Rt△AOB
又Rt△ADF∽Rt△AOB
∴
即
∴AB=5,故BD=3;
(2)显然A(4,0)、B(0,3)
故设解析式为y=kx+3
将(4,0)代入得AB解析式y=- x+3;
x+3;
(3)过D作DH⊥AO于H,
∴DH=BO
∵△ABO∽△ADH
∴DH=
又∵DH∥BO
∴ ,即
,即
∴OH=
∴D点坐标为(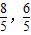 )
)
E点坐标(3,0)
设经过EDO的函数解析式为y=ax2+bx+c.

得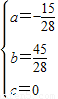
∴所求函数解析式为y=-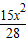 +
+ ;
;
(4)(3)中的顶点为( ,
, ).
).
当x= 时,代入y=-
时,代入y=- x+3=-
x+3=- ×
× +3=
+3=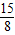 ≠
≠
故(3)的顶点不在直线AB上.
点评:此题考查了二次函数与圆的综合知识,解题时要注意圆的性质,待定系数法的应用,特别是要注意数形结合思想与方程思想的应用.
(2)根据(1)的结论可得A,B的坐标,利用待定系数法可求得经过A、B两点的直线的解析式;
(3)首先求得点D的坐标,将点O,E,D的坐标代入二次函数的一般式,解方程组即可;
(4)求得抛物线的顶点坐标,再代入解析式,看是否左右相等即可.
解答:
 解:(1)设⊙F的半径为r
解:(1)设⊙F的半径为r连接DF,∴BA⊥DF
∵AD切⊙F于D点
∴AD2=AE•AO即22=1•(2r+1)
∴r=
 又Rt△ADF∽Rt△AOB
又Rt△ADF∽Rt△AOB∴

即

∴AB=5,故BD=3;
(2)显然A(4,0)、B(0,3)
故设解析式为y=kx+3
将(4,0)代入得AB解析式y=-
 x+3;
x+3;(3)过D作DH⊥AO于H,
∴DH=BO
∵△ABO∽△ADH
∴DH=

又∵DH∥BO
∴
 ,即
,即
∴OH=

∴D点坐标为(
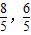 )
)E点坐标(3,0)
设经过EDO的函数解析式为y=ax2+bx+c.

得
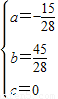
∴所求函数解析式为y=-
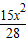 +
+ ;
;(4)(3)中的顶点为(
 ,
, ).
).当x=
 时,代入y=-
时,代入y=- x+3=-
x+3=- ×
× +3=
+3=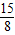 ≠
≠
故(3)的顶点不在直线AB上.
点评:此题考查了二次函数与圆的综合知识,解题时要注意圆的性质,待定系数法的应用,特别是要注意数形结合思想与方程思想的应用.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
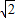 .求BC的长.
.求BC的长.
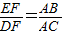 .求证:BD=CE.
.求证:BD=CE.
 ,求BP的长.
,求BP的长.