题目内容
(2004•岳阳)如图,⊙O1与⊙O2外切于P点,过⊙O1上一点B作⊙O1的切线,交⊙O2于C、D,直线BP交⊙O2于点A.(1)求证:∠CBP=∠ADP;
(2)求证:AD2+BC•BD=AB2;
(3)设⊙O2的面积为S2,⊙O1的面积为S1;且S2:S1=9:1,当AD=
 ,求BP的长.
,求BP的长.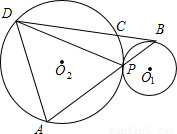
【答案】分析:(1)本题可利用两圆外切的条件进行求解,过P作两圆的公切线,交BD于M.由于MP,MB同为⊙O1的切线,不难得出∠MBP=∠MPB,而∠MPB=∠NPA,根据弦切角定理又可得出∠NPA=∠ADP,将相等的角进行置换后即可得出所求的结论;
(2)所求的线段中,BC•BD=BP•AB,将BC•BD移到等号右边可得出AB2-BC•DB=AB2-BP•AB=AB(AB-BP)=AB•AP,因此只需证明AD2=AB•PA即可,即证明△ADP和△ABD相似.这两个三角形中已知了一个公共角和(1)得出的一组相等角因此两三角形相似,由此得证;
(3)根据两圆的面积比可知两圆的半径比为3:1,要想利用这个条件需要构建相似三角形.连接O1O2,O1B,O2A,不难得出△AO2P∽△BO1P,因此BP与AP的比例关系正好等于两圆的半径比,在根据(2)中证得的AD2=AP•AB即可求出BP的长.
解答: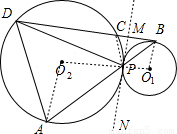 (1)证明:过D点作两圆的公切线PN交BD于M
(1)证明:过D点作两圆的公切线PN交BD于M
∴∠CBD=∠MPB=∠APN
又∵MN为⊙O2的切线
∴∠ADP=∠APN
∴∠CBD=∠ADP;
(2)证明:连接PC
由切割定理得BC•BD=BP•AB
由(1)可知∠CBD=∠ADP
又∵∠A公共
∴△ADP∽△ABD
∴
∴AD2=AB•AP=AB•(AB-BP)=AB2-AB•BP
∴AD2=AB2-BC•BD
即AD2+BC•BD=AB2;
(3)解:设⊙O2的半径为R,⊙O1的半径为r
∴ =
=
∴R:r=3:1
连接AO2,BO1,O1O2,则O1O2经过P点
∴△AO2P∽△BO1P
∴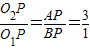
设BP=x
∴AP=3x
从而AB=4x
∵AD2=AP•AB
∴(4 )2=3x•4x
)2=3x•4x
∴x=1,即BP=1.
点评:本题考查了切线的性质、相似三角形的判定和性质、切割线定理等知识点.本题的综合性较强.
(2)所求的线段中,BC•BD=BP•AB,将BC•BD移到等号右边可得出AB2-BC•DB=AB2-BP•AB=AB(AB-BP)=AB•AP,因此只需证明AD2=AB•PA即可,即证明△ADP和△ABD相似.这两个三角形中已知了一个公共角和(1)得出的一组相等角因此两三角形相似,由此得证;
(3)根据两圆的面积比可知两圆的半径比为3:1,要想利用这个条件需要构建相似三角形.连接O1O2,O1B,O2A,不难得出△AO2P∽△BO1P,因此BP与AP的比例关系正好等于两圆的半径比,在根据(2)中证得的AD2=AP•AB即可求出BP的长.
解答:
 (1)证明:过D点作两圆的公切线PN交BD于M
(1)证明:过D点作两圆的公切线PN交BD于M∴∠CBD=∠MPB=∠APN
又∵MN为⊙O2的切线
∴∠ADP=∠APN
∴∠CBD=∠ADP;
(2)证明:连接PC
由切割定理得BC•BD=BP•AB
由(1)可知∠CBD=∠ADP
又∵∠A公共
∴△ADP∽△ABD
∴

∴AD2=AB•AP=AB•(AB-BP)=AB2-AB•BP
∴AD2=AB2-BC•BD
即AD2+BC•BD=AB2;
(3)解:设⊙O2的半径为R,⊙O1的半径为r
∴
 =
=
∴R:r=3:1
连接AO2,BO1,O1O2,则O1O2经过P点
∴△AO2P∽△BO1P
∴
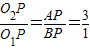
设BP=x
∴AP=3x
从而AB=4x
∵AD2=AP•AB
∴(4
 )2=3x•4x
)2=3x•4x∴x=1,即BP=1.
点评:本题考查了切线的性质、相似三角形的判定和性质、切割线定理等知识点.本题的综合性较强.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
 .求BC的长.
.求BC的长.
 cm,半径r=4cm,则∠BAO= 度.
cm,半径r=4cm,则∠BAO= 度.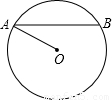
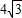 cm,半径r=4cm,则∠BAO= 度.
cm,半径r=4cm,则∠BAO= 度.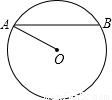
 .求BC的长.
.求BC的长.
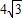 cm,半径r=4cm,则∠BAO= 度.
cm,半径r=4cm,则∠BAO= 度.