题目内容
(2004•岳阳)如图,已知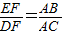 .求证:BD=CE.
.求证:BD=CE.
【答案】分析:作出EM∥AB,构造出△ABC∽△EMC,△DBF∽△EMF,根据相似三角形的性质,建立起BD和CE之间的关系式,即可得出结论.
解答: 证明:过点E作EM∥AB交BF于M,如图
证明:过点E作EM∥AB交BF于M,如图
∵EM∥AB,
∴△ABC∽△EMC.
∴ .
.
∵BD∥EM,
∴△DBF∽△EMF.
∴ .
.
又∵ ,
,
∴ .
.
∴BD=CE.
点评:此题构思极其巧妙,考查了同学们的创造性思维能力.解答此题的关键作出辅助线,建立起各线段之间的联系.
解答:
 证明:过点E作EM∥AB交BF于M,如图
证明:过点E作EM∥AB交BF于M,如图∵EM∥AB,
∴△ABC∽△EMC.
∴
 .
.∵BD∥EM,
∴△DBF∽△EMF.
∴
 .
.又∵
 ,
,∴
 .
.∴BD=CE.
点评:此题构思极其巧妙,考查了同学们的创造性思维能力.解答此题的关键作出辅助线,建立起各线段之间的联系.

练习册系列答案
相关题目
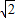 .求BC的长.
.求BC的长.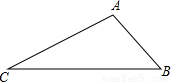
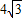 cm,半径r=4cm,则∠BAO= 度.
cm,半径r=4cm,则∠BAO= 度.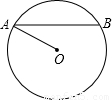
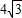 cm,半径r=4cm,则∠BAO= 度.
cm,半径r=4cm,则∠BAO= 度.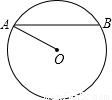
 .求BC的长.
.求BC的长.
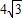 cm,半径r=4cm,则∠BAO= 度.
cm,半径r=4cm,则∠BAO= 度.