题目内容
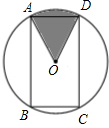 如图,矩形ABCD内接于⊙O,且AB=
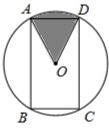
如图,矩形ABCD内接于⊙O,且AB= ,BC=1.则图中阴影部分的面积为________.
,BC=1.则图中阴影部分的面积为________.
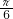
分析:连接OC,根据圆中的有关性质:90°的圆周角所对的弦是直径可知△ABC是直角三角形,根据勾股定理可求得AC的长,从而可求出半径R=
 AC=1,圆心角∠AOD=60°,最后利用扇形的面积公式即可求解.
AC=1,圆心角∠AOD=60°,最后利用扇形的面积公式即可求解.解答:连接OC,如下图所示,

∵矩形ABCD内接于⊙O,
∴∠B=90°,
∴点A,O,C三点在同一条直线上,AC是直径,AC过点O.
Rt△ABC中,AB=
 ,BC=1,
,BC=1,∴AC=2,扇形OAD的半径R=
 AC=1
AC=1∴∠BAC=30°,
∵AB∥DC,
∴∠ACD=30°,
∴∠AOD=60°,
S扇形OAD=
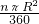 =
= =
=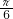 .
.故答案为:
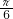 .
.点评:本题主要考查了扇形面积公式的运用,根据圆中的有关性质和勾股定理分别求出圆的直径和半径,再根据直角三角形的特殊性或三角函数求出∠AOD所对应的圆周角的度数是解题的关键,牢记扇形的面积公式:S扇形=
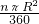 .
. 
练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
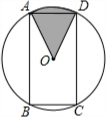 如图,矩形ABCD内接于⊙O,且AB=
如图,矩形ABCD内接于⊙O,且AB=| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,矩形ABCD内接于⊙O,且AB=
如图,矩形ABCD内接于⊙O,且AB=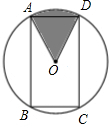 (2012•沙河口区模拟)如图,矩形ABCD内接于⊙O,且AB=
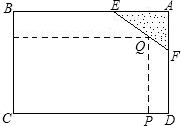
(2012•沙河口区模拟)如图,矩形ABCD内接于⊙O,且AB=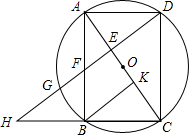 (2012•桂平市三模)如图,矩形ABCD内接于⊙O,AB=3AD,对角线AC中点O为圆心,BK⊥AC,垂足为K.DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.
(2012•桂平市三模)如图,矩形ABCD内接于⊙O,AB=3AD,对角线AC中点O为圆心,BK⊥AC,垂足为K.DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.