题目内容
阅读(1)的推导并填空,然后解答第(2)题.(1)当a<0,∵ax2+bx+c=a(x+
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
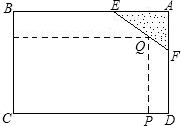
(2)为了绿化城市,我市准备在如图的矩形ABCD内规划一块地面,修建一个矩形草坪PQRC.按计划要求,草坪的两边RC与CP分别在BC和CD上,且草坪不能超过文物保护区△AEF的边界EF.经测量知,AB=CD=100m,BC=AD=80m,AE=30m,AF=20m.应如何确定草坪的位置,才能使草坪占地面积最大又符合设计要求并求出这个最大面积(结果保留到个位,解答时可应用(1)的结论)?
分析:(1)此题检测学生对配方法的掌握情况及运用配方法求最值的原理,可自行配方求A、B,亦可运用顶点坐标公式直接填写.
(2)显然需列出表示草坪面积的关系式.不妨设CP=x,用含x的式子表示面积y.关键是表示PQ,可延长PQ交AE于G,利用△GEQ∽△AEF,先表示GQ的长,再用PG-GQ=PQ,从而求解.
(2)显然需列出表示草坪面积的关系式.不妨设CP=x,用含x的式子表示面积y.关键是表示PQ,可延长PQ交AE于G,利用△GEQ∽△AEF,先表示GQ的长,再用PG-GQ=PQ,从而求解.
解答:解:(1)根据题意:A=
,B=-
.
(2)延长PQ交AE于G,设CP=x,SPQRC=y,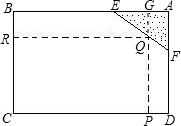
则
=
,GQ=
.
又PQ=PG-GQ=80-
=
,
则y=x•
即:y=-
x2+
x
∴当x=-
=95时,y最大=
≈6017
∴CR=QR=
=63
| 4ac-b2 |
| 4a |
| b |
| 2a |
(2)延长PQ交AE于G,设CP=x,SPQRC=y,

则
| GQ |
| 20 |
| x-(100-30) |
| 30 |
| 2x-140 |
| 3 |
又PQ=PG-GQ=80-
| 2x-140 |
| 3 |
| 380-2x |
| 3 |
则y=x•
| 380-2x |
| 3 |
即:y=-
| 2 |
| 3 |
| 380 |
| 3 |
∴当x=-
| ||
2×(-
|
4×(-
| ||||
4×(-
|
∴CR=QR=
| 380-2×95 |
| 3 |
| 1 |
| 3 |
点评:此题的关键在设其中一边后用它表示另一边的长,要充分运用已知条件,在三角形中构造相似图形,把已知和未知建立联系.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
阅读以下材料并填空:平面上有n个点(n≥2)且任意三个点不在同一直线上,过这些点作直线一共能作出多少条不同的直线?
分析:当仅有两个点时,可连成1条直线;当有3个点时,可连成3条直线;当有4个点时,可连成6条直线,当有5个点时可连成10条直线…
推导:平面上有n个点,因为两点可确定一条直线,所以每个点都可与除本身之外的其余(n-1)个点确定一条直线,即共有
n(n-1)条直线.但因AB与BA是同一条直线,故每一条直线都数了2遍,所以直线的实际总条数为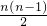 .
.
试结合以上信息,探究以下问题:
平面上有n(n≥3)个点,任意3个点不在同一直线上,过任意3点作三角形,一共能作出多少个不同的三角形?
分析:考察点的个数n和可作出的三角形的个数 sn,发现:(填下表)
| 点的个数 | 可连成的三角形的个数 |
| 3 | ________ |
| 4 | ________ |
| 5 | ________ |
| … | … |
| n | ________ |
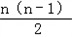 .
.
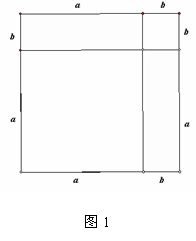 如图1,一个边长为
如图1,一个边长为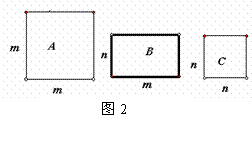 边长为
边长为