��Ŀ����
����Ŀ����ͼ����������![]() �ύ��A��
�ύ��A��![]() ��0����B��
��0����B��![]() ��0�����㣬��
��0�����㣬��![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ������
������![]() ,
,![]() �Ƿ���
�Ƿ���![]() ����������
����������
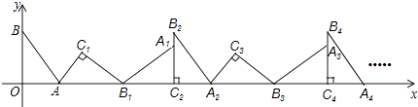
��1���������ߵĽ���ʽ��
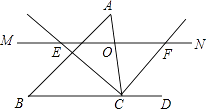
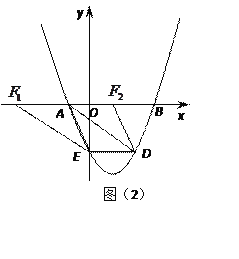
��2����M���߶�AB�ϵ�һ�����㣬����M��MN��BC����AC�ڵ�N������CM������CMN��������ʱ�����M�����ꣻ
��3����D(4��k)�ڣ�1�����������ϣ���EΪ��������һ���㣬��x�����Ƿ���ڵ�F��ʹ��A��D��E��FΪ������ı�����ƽ���ı��Σ�������ڣ�ֱ��д���������������ĵ�F�����꣬�������ڣ���˵�����ɡ�
���𰸡���1��![]() ����2����2��0������3��
����2����2��0������3��![]() .
.
�������������������1������һԪ���η��̽ⷨ�ó�A��B��������꣬�����ý���ʽ������κ�������ʽ��
��2�������ж���MNA�ס�BCA���ó�![]() =
=![]() �������ó���������ֵ��
�������ó���������ֵ��
��3���ֱ���ݵ�AFΪƽ���ı��εı�ʱ��AFƽ���ҵ���DE�뵱AFΪƽ���ı��εĶԽ���ʱ�������ó�����Ҫ��Ĵ𰸣�
���������
��1����![]() ��
��
��![]() ��
�� ![]()
��![]() ��
�� ![]()
�֡������߹���A��B��C��
���������ߵĽ���ʽΪ![]() ��
��
����C��������룬���![]()
�������ߵĽ���ʽΪ![]()
��2�����M������Ϊ��m��0��������N��NH��x���ڵ�H
�ߵ�A������Ϊ��-2��0������B������Ϊ��6��0����
��AB=8��AM=m+2��
��MN��BC��
��. ��MNA�͡�BCA���ƣ�
��![]() ��
��
��![]() ��
��
��![]()
��![]()
![]()
![]()
�൱m=2ʱ�� ![]() �����ֵ4��
�����ֵ4��
��ʱ����M������Ϊ��2��0����
��3���ߵ�D��4��k����������![]() �ϣ�
�ϣ�
�൱x=4ʱ��k=-4��
���D�������ǣ�4��-4����
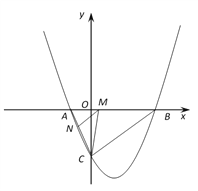
��ͼ��2������AFΪƽ���ı��εı�ʱ��AF![]() DE,AF=DE��
DE,AF=DE��
��D��4��-4������E��0��-4����DE=4��
��F(-6,0)��F(2,0)��
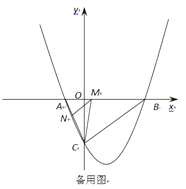
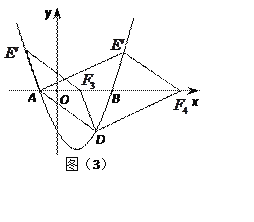
��ͼ��3������AFΪƽ���ı��εĶԽ���ʱ��
��F(n,0)����ƽ���ı��εĶԳ�����Ϊ��![]() ��0����
��0����
��E����������n-6��4����
��E����n-6��4������![]() ����
����
![]()
��� ![]()
��![]() ��
�� ![]() .
.

 ��Ȥ����¹�֪��ϵ�д�
��Ȥ����¹�֪��ϵ�д� Ӣ��СӢ������Ĭдϵ�д�
Ӣ��СӢ������Ĭдϵ�д�