题目内容
作抛物线A关于x轴对称的抛物线B,再将抛物线B向左平移2个单位,向上平移1个单位,得到的抛物线C的函数解析式是y=2(x+1)2-1,则抛物线A所对应的函数表达式是
- A.y=-2(x+3)2-2
- B.y=-2(x+3)2+2
- C.y=-2(x-1)2-2
- D.y=-2(x-1)2+2
D
分析:易得抛物线C的顶点,进而可得到抛物线B的坐标,根据顶点式及平移前后二次项的系数不变可得抛物线B的解析式,而根据关于x轴对称的两条抛物线的顶点的横坐标相等,纵坐标互为相反数,二次项系数互为相反数可得到抛物线A所对应的函数表达式.
解答:易得抛物线C的顶点为(-1,-1),
∵是向左平移2个单位,向上平移1个单位得到抛物线C的,
∴抛物线B的坐标为(1,-2),
可设抛物线B的坐标为y=2(x-h)2+k,代入得:y=2(x-1)2-2,
易得抛物线A的二次项系数为-2,顶点坐标为(1,2),
∴抛物线A的解析式为y=-2(x-1)2+2.
故选D.
点评:讨论两个二次函数的图象的平移问题,只需看顶点坐标是如何平移得到的即可;关于x轴对称的两条抛物线的顶点的横坐标相等,纵坐标互为相反数,二次项系数互为相反数.
分析:易得抛物线C的顶点,进而可得到抛物线B的坐标,根据顶点式及平移前后二次项的系数不变可得抛物线B的解析式,而根据关于x轴对称的两条抛物线的顶点的横坐标相等,纵坐标互为相反数,二次项系数互为相反数可得到抛物线A所对应的函数表达式.
解答:易得抛物线C的顶点为(-1,-1),
∵是向左平移2个单位,向上平移1个单位得到抛物线C的,
∴抛物线B的坐标为(1,-2),
可设抛物线B的坐标为y=2(x-h)2+k,代入得:y=2(x-1)2-2,
易得抛物线A的二次项系数为-2,顶点坐标为(1,2),
∴抛物线A的解析式为y=-2(x-1)2+2.
故选D.
点评:讨论两个二次函数的图象的平移问题,只需看顶点坐标是如何平移得到的即可;关于x轴对称的两条抛物线的顶点的横坐标相等,纵坐标互为相反数,二次项系数互为相反数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
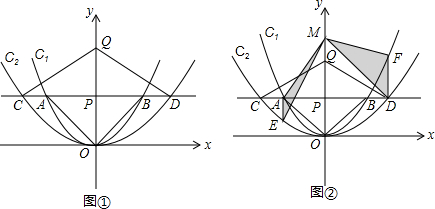
如图①,在平面直角坐标系中,点P(0,m2)(m>0)在y轴正半轴上,过点P作平行于x轴的直线,分别交抛物线C1:y= x2于点A、B,交抛物线C2:y=
x2于点A、B,交抛物线C2:y= x2于点C、D.原点O关于直线AB的对称点为点Q,分别连接OA,OB,QC和QD.
x2于点C、D.原点O关于直线AB的对称点为点Q,分别连接OA,OB,QC和QD.
【猜想与证明】
填表:
| m | 1 | 2 | 3 |
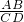 |
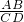 =______.请证明你的猜想.
=______.请证明你的猜想.【探究与应用】
(1)利用上面的结论,可得△AOB与△CQD面积比为______;
(2)当△AOB和△CQD中有一个是等腰直角三角形时,求△CQD与△AOB面积之差;
【联想与拓展】
如图②过点A作y轴的平行线交抛物线C2于点E,过点D作y轴的平行线交抛物线C1于点F.在y轴上任取一点M,连接MA、ME、MD和MF,则△MAE与△MDF面积的比值为______.

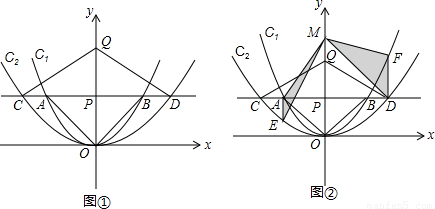
如图①,在平面直角坐标系中,点P(0,m2)(m>0)在y轴正半轴上,过点P作平行于x轴的直线,分别交抛物线C1:y= x2于点A、B,交抛物线C2:y=
x2于点A、B,交抛物线C2:y= x2于点C、D.原点O关于直线AB的对称点为点Q,分别连接OA,OB,QC和QD.
x2于点C、D.原点O关于直线AB的对称点为点Q,分别连接OA,OB,QC和QD.
【猜想与证明】
填表:
由上表猜想:对任意m(m>0)均有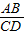 =______.请证明你的猜想.
=______.请证明你的猜想.
【探究与应用】
(1)利用上面的结论,可得△AOB与△CQD面积比为______;
(2)当△AOB和△CQD中有一个是等腰直角三角形时,求△CQD与△AOB面积之差;
【联想与拓展】
如图②过点A作y轴的平行线交抛物线C2于点E,过点D作y轴的平行线交抛物线C1于点F.在y轴上任取一点M,连接MA、ME、MD和MF,则△MAE与△MDF面积的比值为______.
 x2于点A、B,交抛物线C2:y=
x2于点A、B,交抛物线C2:y= x2于点C、D.原点O关于直线AB的对称点为点Q,分别连接OA,OB,QC和QD.
x2于点C、D.原点O关于直线AB的对称点为点Q,分别连接OA,OB,QC和QD.【猜想与证明】
填表:
| m | 1 | 2 | 3 |
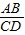 |
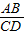 =______.请证明你的猜想.
=______.请证明你的猜想.【探究与应用】
(1)利用上面的结论,可得△AOB与△CQD面积比为______;
(2)当△AOB和△CQD中有一个是等腰直角三角形时,求△CQD与△AOB面积之差;
【联想与拓展】
如图②过点A作y轴的平行线交抛物线C2于点E,过点D作y轴的平行线交抛物线C1于点F.在y轴上任取一点M,连接MA、ME、MD和MF,则△MAE与△MDF面积的比值为______.

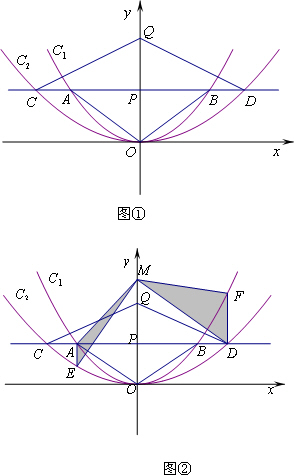
如图①,在平面直角坐标系中,点P(0,m2)(m>0)在y轴正半轴上,过点P作平行于x轴的直线,分别交抛物线C1: 于点A、B,交抛物线C2:
于点A、B,交抛物线C2: 于点C、D.原点O关于直线AB的对称点为点Q,分别连接OA,OB,QC和QD.
于点C、D.原点O关于直线AB的对称点为点Q,分别连接OA,OB,QC和QD.
【猜想与证明】
填表:
|
m |
1 |
2 |
3 |
|
|
|
|
|
由上表猜想:对任意m(m>0)均有 =
.请证明你的猜想.
=
.请证明你的猜想.
【探究与应用】
(1)利用上面的结论,可得△AOB与△CQD面积比为 ;
(2)当△AOB和△CQD中有一个是等腰直角三角形时,求△CQD与△AOB面积之差;
【联想与拓展】
如图②过点A作y轴的平行线交抛物线C2于点E,过点D作y轴的平行线交抛物线C1于点F.在y轴上任取一点M,连接MA、ME、MD和MF,则△MAE与△MDF面积的比值为 .