题目内容
如图①,在平面直角坐标系中,点P(0,m2)(m>0)在y轴正半轴上,过点P作平行于x轴的直线,分别交抛物线C1:y= x2于点A、B,交抛物线C2:y=
x2于点A、B,交抛物线C2:y= x2于点C、D.原点O关于直线AB的对称点为点Q,分别连接OA,OB,QC和QD.
x2于点C、D.原点O关于直线AB的对称点为点Q,分别连接OA,OB,QC和QD.
【猜想与证明】
填表:
| m | 1 | 2 | 3 |
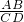 |
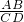 =______.请证明你的猜想.
=______.请证明你的猜想.【探究与应用】
(1)利用上面的结论,可得△AOB与△CQD面积比为______;
(2)当△AOB和△CQD中有一个是等腰直角三角形时,求△CQD与△AOB面积之差;
【联想与拓展】
如图②过点A作y轴的平行线交抛物线C2于点E,过点D作y轴的平行线交抛物线C1于点F.在y轴上任取一点M,连接MA、ME、MD和MF,则△MAE与△MDF面积的比值为______.

解:猜想与证明:
当m=1时,1= x2,1=
x2,1= x2,
x2,
∴x=±2,x=±3,
∴AB=4,CD=6,
∴ ;
;
当m=2时,4= x2,4=
x2,4= x2,
x2,
∴x=±4,x=±6,
∴AB=8,CD=12,
∴ ;
;
当m=3时,9= x2,9=
x2,9= x2,
x2,
∴x=±6,x=±9,
∴AB=12,CD=18,
∴ ;
;
∴填表为
对任意m(m>0)均有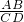 =
= .
.
理由:将y=m2(m>0)代入y= x2,得x=±2m,
x2,得x=±2m,
∴A(-2m,m2),B(2m,m2),
∴AB=4m.
将y=m2(m>0)代入y= x2,得x=±3m,
x2,得x=±3m,
∴C(-3m,m2),D(3m,m2),
∴CD=6m.
∴ ,
,
∴对任意m(m>0)均有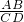 =
= ;
;
探究与运用:
(1)∵O、Q关于直线CD对称,
∴PQ=OP.
∵CD∥x轴,
∴∠DPQ=∠DPO=90°.
∴△AOB与△CQD的高相等.
∵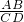 =
= ,
,
∴AB= CD.
CD.
∵S△AOB= AB•PO,S△CQD=
AB•PO,S△CQD= CD•PQ,
CD•PQ,
∴ =
= ,
,
(2)当△AOB为等腰直角三角形时,如图3,
∴PO=PB=m2,AB=2OP
∴m2= m4,
m4,
∴4m2=m4,
∴m1=0,m2=-2,m3=2.
∵m>0,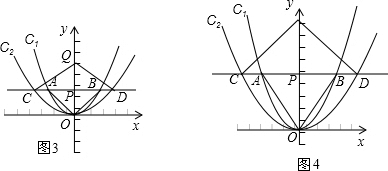
∴m=2,
∴OP=4,AB=8,
∴PD=6,CD=12.
∴S△AOB=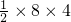 =16
=16
∴S△CQD= =24,
=24,
∴S△CQD-S△AOB=24-16=8.
当△CQD是等腰直角三角形时,如图4,
∴PQ=PO=PD=m2,CD=2QP
∴m2= m4,
m4,
∴9m2=m4,
∴m1=0,m2=-3,m3=3.
∵m>0,
∴m=3,
∴OP=6,AB=12,
∴PQ=9,CD=18.
∴S△AOB= =54
=54
∴S△CQD= =81,
=81,
∴S△CQD-S△AOB=81-54=27;
联想与拓展
由猜想与证明可以得知A(-2m,m2),D(3m,m2),
∵AE∥y轴,DF∥y轴,
∴E点的横坐标为-2m,F点的横坐标为3m,
∴y= (-2m)2,y=
(-2m)2,y= (3m)2,
(3m)2,
∴y= m2,y=
m2,y= m2,
m2,
∴E(-2m, m2),F(3m,
m2),F(3m, m2),
m2),
∴AE=m2- m2=
m2=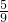 m2,DF=
m2,DF= m2-m2=
m2-m2= m2.
m2.
S△AEM= ×
×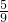 m2•2m=
m2•2m=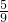 m3,
m3,
S△DFM=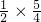 m2•3m=
m2•3m=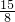 m3.
m3.
∴ =
=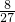 .
.
故答案为: ;
; ;
;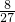 .
.
分析:猜想与证明:
把P点的纵坐标分别代入C1、C2的解析式就可以AB、CD的值,就可以求出结论,从而发现规律得出对任意m(m>0)将y=m2代入两个二次函数的解析式就可以分别表示出AB与CD的值,从而得出均有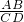 =
= ;
;
探究与证明:
(1)由条件可以得出△AOB与△CQD高相等,就可以得出面积之比等于底之比而得出结论;
(2)分两种情况讨论,当△AOB为等腰直角三角形时,可以求出m的值就可以求出△AOB的面积,从而求出△CQD的面积,就可以求出其差,当△CQD为等腰直角三角形时,可以求出m的值就可以求出△CDQ的面积,进而可以求出结论;
联想与拓展:
由猜想与证明可以得知A、D的坐标,可以求出F、E的纵坐标,从而可以求出AE、DF的值,由三角形的面积公式分别表示出△MAE与△MDF面积,就可以求出其比值.
点评:本题考出了对称轴为y轴的抛物线的性质的运用,由特殊到一般的数学思想的运用,等腰直角三角形的性质的运用,三角形的面积公式的运用,轴对称的性质的运用,在解答本题时运用两个抛物线上的点的特征不变建立方程求解是关键.
当m=1时,1=
 x2,1=
x2,1= x2,
x2,∴x=±2,x=±3,
∴AB=4,CD=6,
∴
 ;
;当m=2时,4=
 x2,4=
x2,4= x2,
x2,∴x=±4,x=±6,
∴AB=8,CD=12,
∴
 ;
;当m=3时,9=
 x2,9=
x2,9= x2,
x2,∴x=±6,x=±9,
∴AB=12,CD=18,
∴
 ;
;∴填表为
| m | 1 | 2 | 3 |
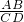 |  |  |  |
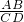 =
= .
.理由:将y=m2(m>0)代入y=
 x2,得x=±2m,
x2,得x=±2m,∴A(-2m,m2),B(2m,m2),
∴AB=4m.
将y=m2(m>0)代入y=
 x2,得x=±3m,
x2,得x=±3m,∴C(-3m,m2),D(3m,m2),
∴CD=6m.
∴
 ,
,∴对任意m(m>0)均有
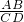 =
= ;
;探究与运用:
(1)∵O、Q关于直线CD对称,
∴PQ=OP.
∵CD∥x轴,
∴∠DPQ=∠DPO=90°.
∴△AOB与△CQD的高相等.
∵
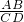 =
= ,
,∴AB=
 CD.
CD.∵S△AOB=
 AB•PO,S△CQD=
AB•PO,S△CQD= CD•PQ,
CD•PQ,∴
 =
= ,
,(2)当△AOB为等腰直角三角形时,如图3,
∴PO=PB=m2,AB=2OP
∴m2=
 m4,
m4,∴4m2=m4,
∴m1=0,m2=-2,m3=2.
∵m>0,

∴m=2,
∴OP=4,AB=8,
∴PD=6,CD=12.
∴S△AOB=
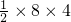 =16
=16∴S△CQD=
 =24,
=24,∴S△CQD-S△AOB=24-16=8.
当△CQD是等腰直角三角形时,如图4,
∴PQ=PO=PD=m2,CD=2QP
∴m2=
 m4,
m4,
∴9m2=m4,
∴m1=0,m2=-3,m3=3.
∵m>0,
∴m=3,
∴OP=6,AB=12,
∴PQ=9,CD=18.
∴S△AOB=
 =54
=54∴S△CQD=
 =81,
=81,∴S△CQD-S△AOB=81-54=27;
联想与拓展
由猜想与证明可以得知A(-2m,m2),D(3m,m2),
∵AE∥y轴,DF∥y轴,
∴E点的横坐标为-2m,F点的横坐标为3m,
∴y=
 (-2m)2,y=
(-2m)2,y= (3m)2,
(3m)2,∴y=
 m2,y=
m2,y= m2,
m2,∴E(-2m,
 m2),F(3m,
m2),F(3m, m2),
m2),∴AE=m2-
 m2=
m2=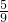 m2,DF=
m2,DF= m2-m2=
m2-m2= m2.
m2.S△AEM=
 ×
×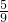 m2•2m=
m2•2m=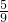 m3,
m3,S△DFM=
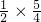 m2•3m=
m2•3m=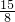 m3.
m3.∴
 =
=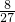 .
.故答案为:
 ;
; ;
;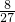 .
.分析:猜想与证明:
把P点的纵坐标分别代入C1、C2的解析式就可以AB、CD的值,就可以求出结论,从而发现规律得出对任意m(m>0)将y=m2代入两个二次函数的解析式就可以分别表示出AB与CD的值,从而得出均有
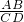 =
= ;
;探究与证明:
(1)由条件可以得出△AOB与△CQD高相等,就可以得出面积之比等于底之比而得出结论;
(2)分两种情况讨论,当△AOB为等腰直角三角形时,可以求出m的值就可以求出△AOB的面积,从而求出△CQD的面积,就可以求出其差,当△CQD为等腰直角三角形时,可以求出m的值就可以求出△CDQ的面积,进而可以求出结论;
联想与拓展:
由猜想与证明可以得知A、D的坐标,可以求出F、E的纵坐标,从而可以求出AE、DF的值,由三角形的面积公式分别表示出△MAE与△MDF面积,就可以求出其比值.
点评:本题考出了对称轴为y轴的抛物线的性质的运用,由特殊到一般的数学思想的运用,等腰直角三角形的性质的运用,三角形的面积公式的运用,轴对称的性质的运用,在解答本题时运用两个抛物线上的点的特征不变建立方程求解是关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
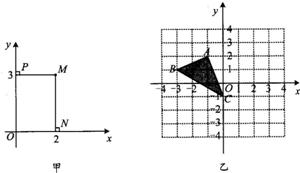 23、在数学上,为了确定平面上点的位置,我们常用下面的方法:如图甲,在平面内画两条互相垂直,并且有公共原点O的数轴,通常一条画成水平,叫x轴,另一条画成铅垂,叫y轴,这样,我们就说在平面上建立了一个平面直角坐标系,这是由法国数学家和哲学家笛卡尔创立的,这样我们就能确定平面上点的位置,例如,要确定点M的位置,只要作MP⊥x轴,MP⊥y轴,设垂足N,P在各自数轴上所表示的数分别为x,y,则x叫做点M的横坐标,y叫做点M的纵坐标,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),(1)△ABC在平面直角坐标系中的位置如图乙,请把△ABC向右平移3个单位,在平面直角坐标系中画出平移后的△A′B′C′;
23、在数学上,为了确定平面上点的位置,我们常用下面的方法:如图甲,在平面内画两条互相垂直,并且有公共原点O的数轴,通常一条画成水平,叫x轴,另一条画成铅垂,叫y轴,这样,我们就说在平面上建立了一个平面直角坐标系,这是由法国数学家和哲学家笛卡尔创立的,这样我们就能确定平面上点的位置,例如,要确定点M的位置,只要作MP⊥x轴,MP⊥y轴,设垂足N,P在各自数轴上所表示的数分别为x,y,则x叫做点M的横坐标,y叫做点M的纵坐标,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),(1)△ABC在平面直角坐标系中的位置如图乙,请把△ABC向右平移3个单位,在平面直角坐标系中画出平移后的△A′B′C′;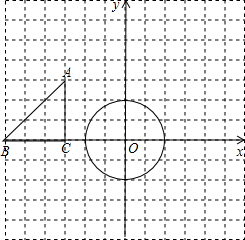 在平面直角坐标系中,将一块腰长为
在平面直角坐标系中,将一块腰长为
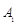 为旋转中心时,点
为旋转中心时,点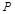 绕着点
绕着点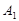 旋转180°得到
旋转180°得到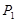 点,点
点,点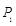 再绕着点
再绕着点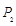 点,这时点
点,这时点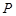 与点
与点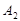 为旋转中心时,点
为旋转中心时,点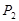 点,点
点,点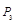 点,点
点,点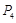 点,小明发现P、
点,小明发现P、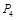 两点关于点
两点关于点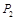 中心对称.
中心对称.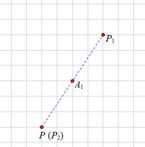
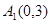 、
、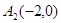 、
、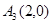 为旋转中心时,点
为旋转中心时,点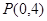 绕着点
绕着点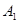 旋转180°得到
旋转180°得到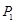 点;点
点;点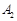 旋转180°得到
旋转180°得到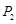 点;点
点;点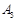 旋转180°得到
旋转180°得到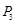 点;点
点;点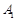 旋转180°得到点
旋转180°得到点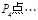 . 继续如此操作若干次得到点
. 继续如此操作若干次得到点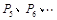 ,则点
,则点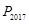 的坐为.
的坐为.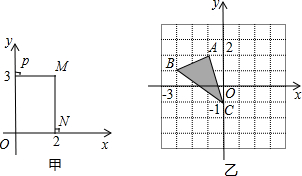 ,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),
,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),