题目内容
对非负实数x“四舍五入”到个位的值记为<x>
即:当n为非负整数时,如果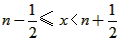 ,则<x>
,则<x>=n,
如:<0>=<0.48>=0,<0.64>=<1.493>=1,<2>=2,<3.5>=<4.12>=4,…
试解决下列问题:
(1)填空:①<π>=____(π为圆周率);
②如果<2x-1>=3,则实数x的取值范围为____;
(2)①当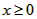 ;m为非负整数时,求证:<x+m>=m+<x>;
;m为非负整数时,求证:<x+m>=m+<x>;
②举例说明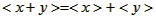 不恒成立;
不恒成立;
(3)求满足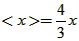 的所有非负实数x的值;
的所有非负实数x的值;
(4)设n为常数,且为正整数,函数y=x2-x+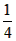 的自变量x在n≤x≤n+1范围内取值时,函数值y为整数的个数记为a;满足
的自变量x在n≤x≤n+1范围内取值时,函数值y为整数的个数记为a;满足 的所有整数k的个数记为b,求证:a=b=2n。
的所有整数k的个数记为b,求证:a=b=2n。
即:当n为非负整数时,如果
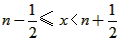 ,则<x>
,则<x>如:<0>=<0.48>=0,<0.64>=<1.493>=1,<2>=2,<3.5>=<4.12>=4,…
试解决下列问题:
(1)填空:①<π>=____(π为圆周率);
②如果<2x-1>=3,则实数x的取值范围为____;
(2)①当
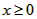 ;m为非负整数时,求证:<x+m>=m+<x>;
;m为非负整数时,求证:<x+m>=m+<x>;②举例说明
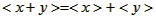 不恒成立;
不恒成立;(3)求满足
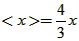 的所有非负实数x的值;
的所有非负实数x的值;(4)设n为常数,且为正整数,函数y=x2-x+
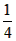 的自变量x在n≤x≤n+1范围内取值时,函数值y为整数的个数记为a;满足
的自变量x在n≤x≤n+1范围内取值时,函数值y为整数的个数记为a;满足 的所有整数k的个数记为b,求证:a=b=2n。
的所有整数k的个数记为b,求证:a=b=2n。解:(1)①3;②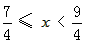
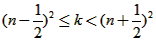 ;
;
(2)①证明:
设<x>=n,
则n-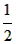 ≤x<n+
≤x<n+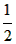 ,n为非负整数;
,n为非负整数;
又(n+m)-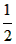 ≤x+m<(n+m)+
≤x+m<(n+m)+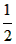 ,且m+n为非负整数,
,且m+n为非负整数,
∴<x+m>=n+m=m+<x>;
②举反例:<0.6>+<0.7>=1+1=2,
而<0.6+0.7>=<1.3>=1,
∴<0.6>+<0.7>≠<0.6+0.7>,
∴<x>+<y>=<x+y>不一定成立;
(3)作y=<x>,y=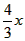 的图象,如图
的图象,如图
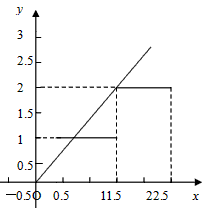
y=<x>的图象与y=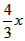 图象交于点(0,0)、
图象交于点(0,0)、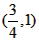 、
、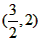 ,
,
∴x=0, ;
;
(4)∵函数y=x2-x+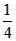 =(x-
=(x-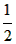 )2,n为整数,
)2,n为整数,
当n≤x<n+1时,y随x的增大而增大,
∴(n-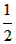 )2≤y<(n+1-
)2≤y<(n+1-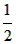 )2,
)2,
即(n-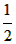 )2≤y<(n+
)2≤y<(n+ )2,①
)2,①
∴n2-n+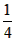 ≤y<n2+n+
≤y<n2+n+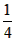 ,
,
∵y为整数,
∴y=n2-n+1,n2-n+2,n2-n+3,…,n2-n+2n,共2n个y,
∴a=2n②,
则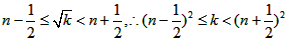 ,③
,③
比较①,②,③得:a=b=2n。
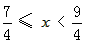
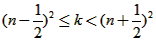 ;
;(2)①证明:
设<x>
则n-
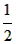 ≤x<n+
≤x<n+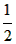 ,n为非负整数;
,n为非负整数;又(n+m)-
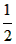 ≤x+m<(n+m)+
≤x+m<(n+m)+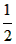 ,且m+n为非负整数,
,且m+n为非负整数,②举反例:<0.6>+<0.7>=1+1=2,
而<0.6+0.7>=<1.3>=1,
∴<0.6>+<0.7>≠<0.6+0.7>,
∴<x>
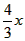 的图象,如图
的图象,如图
y=<x>
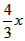 图象交于点(0,0)、
图象交于点(0,0)、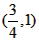 、
、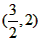 ,
,∴x=0,
 ;
;(4)∵函数y=x2-x+
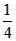 =(x-
=(x-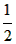 )2,n为整数,
)2,n为整数,当n≤x<n+1时,y随x的增大而增大,
∴(n-
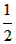 )2≤y<(n+1-
)2≤y<(n+1-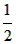 )2,
)2,即(n-
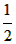 )2≤y<(n+
)2≤y<(n+ )2,①
)2,①∴n2-n+
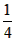 ≤y<n2+n+
≤y<n2+n+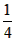 ,
,∵y为整数,
∴y=n2-n+1,n2-n+2,n2-n+3,…,n2-n+2n,共2n个y,
∴a=2n②,
则
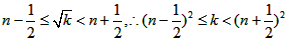 ,③
,③比较①,②,③得:a=b=2n。

练习册系列答案
相关题目
 ,则<x>=n,如<0.46>=0,<3.67>=4。给出下列关于<x>的结论:
,则<x>=n,如<0.46>=0,<3.67>=4。给出下列关于<x>的结论: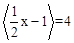 ,则实数x的取值范围是
,则实数x的取值范围是 ;
; ;
; 。
。