题目内容
对非负实数x“四舍五入”到个位的值记为<x>,即:当n为非负整数时,如果n-
| 1 |
| 2 |
| 1 |
| 2 |
如:<0>=<0.48>=0,<0.64>=<1.493>=1,<2>=2,<3.5>=<4.12>=4,…
试解决下列问题:
(1)填空:①<π>=
②如果<2x-1>=3,则实数x的取值范围为
(2)①当x≥0,m为非负整数时,求证:<x+m>=m+<x>;
②举例说明<x+y>=<x>+<y>不恒成立;
(3)求满足<x>=
| 4 |
| 3 |
(4)设n为常数,且为正整数,函数y=x2-x+
| 1 |
| 4 |
| k |
分析:(1)π的十分位为1,应该舍去,所以精确到个位是3;如果精确数是3,那么这个数应在2.5和3.5之间,包括2.5,不包括3.5,让2.5≤2x-1<3.5,解不等式即可;
(2)①分别表示出<x+m>和<x>,即可得到所求不等式;②举出反例说明即可,譬如稍微超过0.5的两个数相加;
(3)
x为整数,设这个整数为k,易得这个整数应在应在k-
和k+
之间,包括k-
,不包括k+
,求得整数k的值即可求得x的非负实数的值;
(4)易得二次函数的对称轴,那么可求得二次函数的函数值在相应的自变量的范围内取值,进而求得相应的a的个数;利用所给关系式易得
的整数个数为2n,由此得证.
(2)①分别表示出<x+m>和<x>,即可得到所求不等式;②举出反例说明即可,譬如稍微超过0.5的两个数相加;
(3)
| 4 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(4)易得二次函数的对称轴,那么可求得二次函数的函数值在相应的自变量的范围内取值,进而求得相应的a的个数;利用所给关系式易得
| k |
解答:解:(1)①3;
②由题意得:2.5≤2x-1<3.5,解得:
≤x<
;
(2)①证明:设<x>=n,则n-
≤x<n+
,n为非负整数;
∴(n+m)-
≤x+m<(n+m)+
,且n+m为非负整数,
∴<x+m>=n+m=m+<x>.
②举反例:<0.6>+<0.7>=1+1=2,而<0.6+0.7>=<1.3>=1,
∴<0.6>+<0.7>≠<0.6+0.7>,
∴<x+y>=<x>+<y>不一定成立;
(3)∵x≥0,
x为整数,设
x=k,k为整数,
则x=
k,
∴<
k>=k,
∴k-
≤
k<k+
,k≥0,
∵O≤k≤2,
∴k=0,1,2,
∴x=0,
,
.
(4)∵函数y=x2-x+
=(x-
)2,n为整数,
当n≤x<n+1时,y随x的增大而增大,
∴(n-
)2≤y<(n+1-
)2,即(n-
)2≤y<(n+
)2,①
∴n2-n+
≤y<n2+n+
,∵y为整数,
∴y=n2-n+1,n2-n+2,n2-n+3,…,n2-n+2n,共2n个y,
∴a=2n,②
∵k>0,<
>=n,
则n-
≤
<n+
,∴(n-
)2≤k<(n+
)2,③
比较①,②,③得:a=b=2n.
②由题意得:2.5≤2x-1<3.5,解得:
| 7 |
| 4 |
| 9 |
| 4 |
(2)①证明:设<x>=n,则n-
| 1 |
| 2 |
| 1 |
| 2 |
∴(n+m)-
| 1 |
| 2 |
| 1 |
| 2 |
∴<x+m>=n+m=m+<x>.
②举反例:<0.6>+<0.7>=1+1=2,而<0.6+0.7>=<1.3>=1,
∴<0.6>+<0.7>≠<0.6+0.7>,
∴<x+y>=<x>+<y>不一定成立;
(3)∵x≥0,
| 4 |
| 3 |
| 4 |
| 3 |
则x=
| 3 |
| 4 |
∴<
| 3 |
| 4 |
∴k-
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
∵O≤k≤2,
∴k=0,1,2,
∴x=0,
| 3 |
| 4 |
| 3 |
| 2 |
(4)∵函数y=x2-x+
| 1 |
| 4 |
| 1 |
| 2 |
当n≤x<n+1时,y随x的增大而增大,
∴(n-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴n2-n+
| 1 |
| 4 |
| 1 |
| 4 |
∴y=n2-n+1,n2-n+2,n2-n+3,…,n2-n+2n,共2n个y,
∴a=2n,②
∵k>0,<
| k |
则n-
| 1 |
| 2 |
| k |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
比较①,②,③得:a=b=2n.
点评:解决本题的关键是理解:对非负实数x“四舍五入”到个位的值记为<x>,即:当n为非负整数时,如果n-
≤x<n+
,则<x>=n.
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
相关题目
 ,则<x>=n,如<0.46>=0,<3.67>=4。给出下列关于<x>的结论:
,则<x>=n,如<0.46>=0,<3.67>=4。给出下列关于<x>的结论: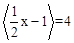 ,则实数x的取值范围是
,则实数x的取值范围是 ;
; ;
; 。
。