题目内容
深化理解:对非负实数x“四舍五入”到个位的值记为<x>,
即:当n为非负整数时,如果n-
| 1 |
| 2 |
| 1 |
| 2 |
如:<0>=<0.48>=0,<0.64>=<1.493>=1,<2>=2,<3.5>=<4.12>=4,…
试解决下列问题:
(1)填空:<π>=
(2)如果<2x-1>=3,求实数x的取值范围.
分析:根据题意可看出对非负实数x“四舍五入”到个位的值记为<x>,所以看看四舍五入后,个位数就是要求的值.
(1)因为π≈3.14,所以四舍五入后的个位数就为所求.
(2)近似数值到3的范围是2.5到3.5的范围,包括2.5不包括3.5,可列不等式组求解.
(1)因为π≈3.14,所以四舍五入后的个位数就为所求.
(2)近似数值到3的范围是2.5到3.5的范围,包括2.5不包括3.5,可列不等式组求解.
解答:解:(1)因为π≈3.14,所以四舍五入后的个位数为3.
故答案为:3.(2分)
(2)
.
解得:
≤x<
(6分)
故答案为:3.(2分)
(2)
|
解得:
| 7 |
| 4 |
| 9 |
| 4 |
点评:本题考查理解题意的能力,关键是看到所得值是个位数四舍五入后的值,问题可得解.

练习册系列答案
相关题目
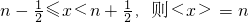 .
.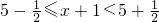 ,所以实数x的取值范围为
,所以实数x的取值范围为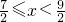 .
.