题目内容
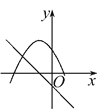
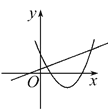
【题目】已知:如图,二次函数y=x2+bx+c的图象过点A(1,0)和C(0,﹣3)
(1)求这个二次函数的解析式;
(2)如果这个二次函数的图象与x轴的另一个交点为B,求线段AB的长.
(3)在这条抛物线上是否存在一点P,使△ABP的面积为8?若存在,求出点P的坐标;若不存在,请说明理由.

【答案】(1)二次函数的解析式为![]() ;(2)
;(2)![]() ;(3)存在,点
;(3)存在,点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() .
.
【解析】试题分析:(1)利用待定系数法把A(1,0),C(0,-3)代入二次函数y=x2+bx+c中,即可算出b、c的值,进而得到函数解析式是y=x2+2x-3;
(2)首先求出A、B两点坐标,再算出AB的长;
(3)设P(m,n),根据△ABP的面积为8可以计算出n的值,然后再利用二次函数解析式计算出m的值即可得到P点坐标.
试题解析:
(1)依题意把![]() ,
, ![]() 代入
代入![]() 得:
得:
![]() ,解得:
,解得: ![]() ,
,
∴ 该二次函数的解析式为![]() ;
;
(2)令![]() ,则
,则![]() ,
,
解之得: ![]() ,
, ![]() ,
,
∴ 点B坐标为(-3,0),
又∵ ![]() ,
,
∴ ![]() ;
;
(3)存在. 设点![]() 坐标为
坐标为![]() ,由
,由![]() 得:
得: ![]() ,解得:
,解得: ![]() ,
,
分两种情况讨论:
①当![]() 时,点
时,点![]() 坐标为
坐标为![]() ,则
,则![]() ,
,
解得: ![]() ,
, ![]() ,
,
∴ ![]() ,
, ![]() ;
;
②当![]() 时,点
时,点![]() 坐标为
坐标为![]() ,则
,则![]() ,
,
解得: ![]() , ∴
, ∴ ![]() ,
,
综上所述,在这条抛物线上存在一点![]() ,使△
,使△![]() 的面积为
的面积为 ![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目