题目内容
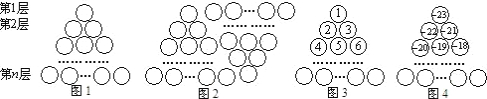
图1是由若干个小圆圈堆成的一个图案,最上面一层有2个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.完成下列问题:
(1)每一层的圆圈个数与层数的关系为:
| 层数 | 1 | 2 | 3 | … | n |
| 每层圆圈个数 | … |
将图1倒置后与原图1拼成图2的形状,则图2中每层圆圈个数为________;n层圆圈总数为________;由于图2中圆圈个数是图1中的________倍,可以得出图1中所有圆圈的个数为________.
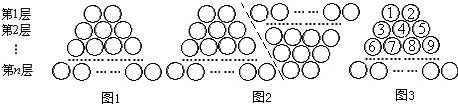
(3)假设图1中的圆圈共有10层,我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数1,2,3,4,…,则最底层从左边数第三个圆圈中的数是________.
解:(1)填写如下:
(2)将图1倒置后与原图1拼成图2的形状,则图2中每层圆圈个数为n+3;n层圆圈总数为n;由于图2中圆圈个数是图1中的2倍,可以得出图1中所有圆圈的个数为 .
.
(3)∵当n=9时,共有圆圈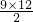 =54个圆圈,
=54个圆圈,
∴第10层从左起第三个圆圈的数字为57.
分析:(1)按照每一层圆圈比上一层多一个的规律即可完成表格;
(2)根据得到的每层的圆圈的个数及层数即可求得总数,除以2即可得到图一中圆圈的个数;
(3)首先根据层数前9层的个数即可得到答案.
点评:考查了规律型:图形的变化.本题是一道找规律的题目,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.
| 层数 | 1 | 2 | 3 | … | n |
| 每层圆圈个数 | 2 | 3 | 4 | … | n+1 |
 .
.(3)∵当n=9时,共有圆圈
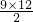 =54个圆圈,
=54个圆圈,∴第10层从左起第三个圆圈的数字为57.
分析:(1)按照每一层圆圈比上一层多一个的规律即可完成表格;
(2)根据得到的每层的圆圈的个数及层数即可求得总数,除以2即可得到图一中圆圈的个数;
(3)首先根据层数前9层的个数即可得到答案.
点评:考查了规律型:图形的变化.本题是一道找规律的题目,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.

练习册系列答案
相关题目