Question

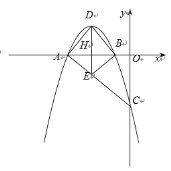
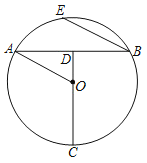
【题目】如图，已知AB是⊙O的弦，点C在⊙O上，且，联结AO，CO，并延长CO交弦AB于点D，AB＝4，CD＝6．

（1）求∠OAB的大小；

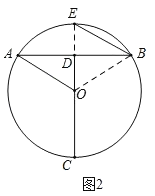
（2）若点E在⊙O上，BE∥AO，求BE的长．

Answer 1

【答案】（1）30°；（2）4．

【解析】

（1）连接OB，证OD垂直平分AB，在Rt△AOD中通过解直角三角形可求出∠OAB的度数；

（2）连接OE，证△OBE是等边三角形，即可知BE的长度等于半径．

解：（1）如图1，连接OB，

∵，

∴∠AOC＝∠BOC，

∴180°﹣∠AOC＝180°﹣∠BOC，

∴∠AOD＝∠BOD，

∵OA＝OB，

∴OD垂直平分AB，

∴AD＝BD＝AB＝2，

设⊙O的半径为r，则OD＝6﹣r，

在Rt△AOD中，AO2＝AD2+OD2，

∴r2＝（2）2+（6﹣r）2，

解得，r＝4，

∴cos∠OAD＝，

∴∠OAD＝30°，

即∠OAB＝30°；

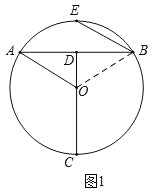
（2）如图2，连接OE，

由（1）知，∠OAB＝30°，

∵OB＝OA，

∴∠OBA＝∠OAB＝30°，

∵EB∥AO，

∴∠EBD＝∠OAB＝30°，

∴∠EBO＝∠EBD+∠OBA＝60°，

∵OE＝OB，

∴△OEB是等边三角形，

∴BE＝r＝4．