��Ŀ����
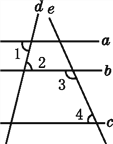
����Ŀ���ڡ�ABC��,��ACB=900��AC=BC=4��MΪAB���е�,D������BC��һ������, ����AD,���߶�AD�Ƶ�A��ʱ����ת900���õ��߶�AE,����DE,NΪDE���е�, ����AN,MN.
(1)��ͼ1����BD=2ʱ,AN= ,NM= ,MN��AB��λ�ù�ϵ�� .
(2)��4<BD<8ʱ.
�������ⲹȫͼ2��
���ж�(1)��MN��AB��λ�ù�ϵ�Ƿ����仯����֤����Ľ���.
(3)����ME���ڵ�D�˶��Ĺ����У���BD/�ij�Ϊ��ֵʱ��ME�ij���С����Сֵ�Ƕ��٣���ֱ��д�����.

���𰸡���1��![]() ����ֱ��2����ͼ�μ�������λ�ù�ϵ���䣬
����ֱ��2����ͼ�μ�������λ�ù�ϵ���䣬 ![]()
�������������������1��������֪�����õ�CD=2�����ݹ��ɶ����õ�AD=![]() =2
=2![]() ��������ת�����ʵõ���ADE�ǵ���ֱ�������Σ����DE=
��������ת�����ʵõ���ADE�ǵ���ֱ�������Σ����DE=![]() AD=2
AD=2![]() ������ֱ�������ε����ʵõ�AN=
������ֱ�������ε����ʵõ�AN=![]() DE=
DE=![]() ��AM=
��AM=![]() AB=2
AB=2![]() ���Ƴ���ACD�ס�AMN���������������ε����ʼ��ɵõ����ۣ���2���ٸ������ⲹȫͼ�μ��ɣ��ڸ��ݵ���ֱ�������ε����ʵõ���CAB=��B=45�㣬��á�CAN+��NAM=45�������ת�����ʵõ�AD=AE����DAE=90�㣬�Ƴ���ANM��ADC�������������ε����ʵõ���AMN=��ACD�����ɵõ����ۣ���3������ME��EB����M��MG��EB��G����A��AK��AB��BD���ӳ�����K���õ���AKB����ֱ�������Σ��Ƴ���ADK�ա�ABE������ȫ�������ε����ʵõ���ABE=��K=45�㣬֤�á�BMG�ǵ���ֱ�������Σ����BC=4��AB=4
���Ƴ���ACD�ס�AMN���������������ε����ʼ��ɵõ����ۣ���2���ٸ������ⲹȫͼ�μ��ɣ��ڸ��ݵ���ֱ�������ε����ʵõ���CAB=��B=45�㣬��á�CAN+��NAM=45�������ת�����ʵõ�AD=AE����DAE=90�㣬�Ƴ���ANM��ADC�������������ε����ʵõ���AMN=��ACD�����ɵõ����ۣ���3������ME��EB����M��MG��EB��G����A��AK��AB��BD���ӳ�����K���õ���AKB����ֱ�������Σ��Ƴ���ADK�ա�ABE������ȫ�������ε����ʵõ���ABE=��K=45�㣬֤�á�BMG�ǵ���ֱ�������Σ����BC=4��AB=4![]() ��MB=2
��MB=2![]() ����ME��MG�����ǵõ���ME=MGʱ��ME��ֵ��С�����ݵ����������ɵõ����ۣ�
����ME��MG�����ǵõ���ME=MGʱ��ME��ֵ��С�����ݵ����������ɵõ����ۣ�
���������(1)�ߡ�ACB=90����AC=BC=4��BD=2��
��CD=2��
��AD=![]() =2
=2![]() ��
��
�߽��߶�AD�Ƶ�A��ʱ����ת90��õ��߶�AE��
���ADE�ǵ���ֱ�������Σ�
��DE=![]() AD=2
AD=2![]() ��
��
��NΪED���е㣬
��AN=![]() DE=
DE=![]() ��
��
��MΪAB���е㣬
��AM=![]() AB=2
AB=2![]() ��
��
��![]() ��
�� ![]() ��
��
��![]() =
= ![]() ��
��
�ߡ�CAB=��DAN=45�㣬
���CAD=��MAN��
���ACD�ס�AMN��
���AMN=��C=90�㣬
��MN��AB��
�ʴ�Ϊ�� ![]() ����ֱ��
����ֱ��
(2)�ٲ�ȫͼ����ͼ2��ʾ,

��(1)��NM��AB��λ�ù�ϵ�������仯��
���ɣ��ߡ�ACB=90�㣬AC=BC��
���CAB=��B=45�㣬
���CAN+��NAM=45�㣬
���߶�AD�Ƶ�A��ʱ����ת90��õ��߶�AE��
��AD=AE,��DAE=90�㣬
��NΪED���е㣬
���DAN=12��DAE=45�㣬AN��DE��
���CAN+��DAC=45�㣬
���NAM=��DAC,��Rt��AND��,ANAD=cos��DAN=cos45��=2![]() ��
��
ͬ��ACAB=2 ![]() ��
��
��![]() =
= ![]() ����
����
�ߡ�DAC=45����CAN=��MAN��
���ANM�ס�ADC��
���AMN=��ACD��
��D��BC���ӳ����ϣ�
���ACD=180����ACB=90�㣬
���AMN=90�㣬
��MN��AB��
(3)����ME��EB����M��MG��EB��G����A��AK��AB��BD���ӳ�����K��

���AKB����ֱ�������Σ�
�ڡ�ADK���ABE�У�
 ��
��
���ADK�ա�ABE��
���ABE=��K=45�㣬
���BMG�ǵ���ֱ�������Σ�
��BC=4��
��AB=4![]() ,MB=2
,MB=2![]() ��
��
��MG=2��
�ߡ�G=90�㣬
��MEMG��
�൱ME=MGʱ��ME��ֵ��С��
��ME=BE=2��
��DK=BE=2��
��CK=BC=4��
��CD=2��
��BD=6��
��BD�ij�Ϊ6ʱ��ME�ij���С����Сֵ��2.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�