题目内容
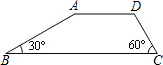如图，已知梯形ABCD中，AD∥BC，∠B=30°，∠C=60°，AD=4，AB=3| 3 |
分析：过A作AE∥CD，把梯形分成平行四边形和直角三角形，利用平行四边形的对边相等得到CE=AD，所以BE可以求出，在直角三角形中，根据∠B=30°，利用勾股定理求出BE，BC的长也就可以求出了．
解答：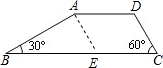
解：如图，过A作AE∥CD交BC于点E，
∵AD∥BC，∴四边形AECD是平行四边形，
∴CE=AD=4，
∵∠B=30°，∠C=60°，
∴∠BAE=90°，
∴AE=
BE（直角三角形30°角所对的直角边等于斜边的一半），
在Rt△ABE中，BE2=AB2+AE2，
即BE2=（3
）2+（
BE）2，
BE2=27+
BE2，
BE2=36，
解得BE=6，
∴BC=BE+EC=6+4=10．
故答案为：10．
解：如图，过A作AE∥CD交BC于点E，∵AD∥BC，∴四边形AECD是平行四边形，
∴CE=AD=4，
∵∠B=30°，∠C=60°，
∴∠BAE=90°，
∴AE=
| 1 |
| 2 |
在Rt△ABE中，BE2=AB2+AE2，
即BE2=（3
| 3 |
| 1 |
| 2 |
BE2=27+
| 1 |
| 4 |
BE2=36，
解得BE=6，
∴BC=BE+EC=6+4=10．
故答案为：10．
点评：通过作腰的平行线，把梯形分成平行四边形和直角三角形，再利用直角三角形30°角所对的直角边等于斜边的一半和勾股定理求解，考虑本题的突破口在于两个已知角的和是90°．
练习册系列答案
百年学典课时学练测系列答案
仁爱英语同步练习册系列答案
相关题目
9、如图，已知梯形ABCD中，AD∥BC，BE平分∠ABC，BE⊥CD，∠A=110°，AD=3，AB=5，则BC的长为（ ）
点到达终点时，另一点也随之停止．过Q作QD∥AB交AC于点D，连接PD，设运动时间为t秒时，四边形BQDP的面积为s．
（2007•遂宁）如图，已知等腰△ABC的面积为4cm2，点D、E分别是AB、AC边的中点，则梯形DBCE的面积为