题目内容
【题目】在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC.
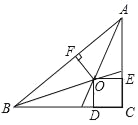
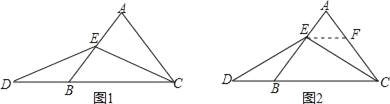
(1)(观察猜想)当点E在AB的中点时,如图1,过点E作EF∥BC,交AC于点F,观察猜想得到线段AE与DB的大小关系是 ;
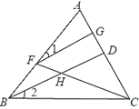
(2)(探究证明)当点E不是AB的中点时,如图2,上述结论是否成立,如果成立,请写出解答过程,如果不成立,请说明理由;
(3)(拓展延伸)在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC,若△ABC的边长为2,AE=1,求CD的长(请直接写出结果).

【答案】(1)AE=DB;(2)AE=DB,理由见解析;(3)CD线段 的长度是3或1.
【解析】
(1)根据等边三角形性质和等腰三角形的性质求出∠D=∠ECB=30°,求出∠DEB=30°,求出BD=BE即可;
(2)过E作EF∥BC交AC于F,求出等边三角形AEF,证△DEB和△ECF全等,求出BD=EF即可;
(3)根据(2)的结论计算即可.
(1)如图1,∵△ABC是等边三角形,点E是AB的中点,
∴CE平分∠ACB,CE⊥AB,
∴∠ACB=60°,∠BEC=90°,AE=BE,
又∵ED=EC,
∴∠D=∠ECB=30°,
∴∠DEC=120°,
∴∠DEB=120°﹣90°=30°,
∴∠D=∠DEB=30°,
∴BD=BE=AE,即AE=DB.
故答案为:AE=DB.
(2)如图2,当点E为AB上任意一点时,AE=DB.理由如下:
如图2,过E作EF∥BC交AC于F,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠A=60°,AB=AC=BC,
∴∠AEF=∠ABC=60°,∠AFE=∠ACB=60°,即∠AEF=∠AFE=∠A=60°,
∴△AEF是等边三角形,
∴AE=EF=AF,
∵∠ABC=∠ACB=∠AFE=60°,
∴∠DBE=∠EFC=120°,∠D+∠BED=∠FCE+∠ECD=60°,
∵DE=EC,
∴∠D=∠ECD,
∴∠BED=∠ECF,
在△DEB和△ECF中,
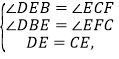
∴△DEB≌△ECF(AAS),
∴BD=EF=AE,即AE=BD,
(3)如图2,当点E在线段AB上时,CD=BC+BD=BC+AE=2+1=3.
当点E不在线段AB上时,CD=BC﹣AE=2﹣1=1.
综上所述,CD线段的长度是3或1.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案【题目】父亲告诉小明:“距离地面越高,温度越低,”并给小明出示了下面的表格。
距离地面高度(千米) | 0 | 1 | 2 | 3 | 4 | 5 |
温度(℃) | 20 | 14 | 8 | 2 |
|
|
根据上表,父亲还给小明出了下面几个问题,你和小明一起回答。
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用h表示距离地面的高度,用t表示温度,那么随着h的变化,t是怎么变化的?
(3)你能猜出距离地面6千米的高空温度是多少吗?