题目内容
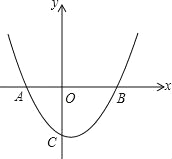
【题目】如图，二次函数图象经过A（﹣3，0）、B（4，0）、C（0，﹣4）三点．
（1）求该抛物线的解析式；
（2）求该抛物线的对称轴；
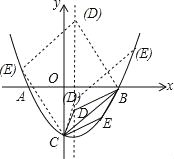
（3）该抛物线的对称轴上有一点D，在该抛物线上是否存在一点E，使得以D、E、B、C为顶点的四边形是平行四边形？若存在，求出点E的坐标；若不存在，请说明理由．
【答案】（1）y=
x2﹣
x﹣4；（2）x=
；（3）存在，点E的坐标为（
，﹣
）、（
，
）或（﹣
，
）．
【解析】
试题分析：（1）设抛物线的解析式为y=ax2+bx+c（a≠0），根据点A、B、C的坐标利用待定系数法即可求出抛物线的解析式；（2）根据二次函数的解析式结合二次函数的性质即可得出抛物线的对称轴；（3）假设存在，分线段BC为对角线以及BC为边两种情况考虑，根据点B、C、D的坐标结合平行四边形的性质即可得出点E的坐标，利用二次函数图象上点的坐标特征即可求出点E的坐标，此题得解．
试题解析：（1）设抛物线的解析式为y=ax2+bx+c（a≠0），将A（﹣3，0）、B（4，0）、C（0，﹣4）代入y=ax2+bx+c（a≠0）中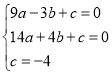得：
，解得：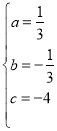
，∴该抛物线的解析式为y=
x2﹣
x﹣4．（2）∵抛物线的解析式为y=x2﹣x﹣4，∴该抛物线的对称轴为x=﹣
=
．（3）假设存在，∵点D在抛物线的对称轴上，∴设点D的坐标为（
，m）．以D、E、B、C为顶点的四边形是平行四边形分两种情况（如图所示）：①当线段BC为对角线时，∵B（4，0）、C（0，﹣4）、D（，m），∴点E的坐标为（4﹣， ﹣
，﹣4﹣m），∵点E在抛物线y=x2﹣x﹣4上，∴﹣4﹣m=
×
﹣×
﹣4=﹣
，此时点E的坐标为（
，﹣
）；②当线段BC为边时，∵B（4，0）、C（0，﹣4）、D（，m），∴点E的坐标为（+4，m+4）或（﹣4，m+4），既（
，m+4）或（﹣，m+4）．∵点E在抛物线y=x2﹣x﹣4上，∴m+4=×
﹣×
﹣4=
或m+4=×
﹣×（﹣）﹣4=
，此时点E的坐标为（
，）或（﹣，）．综上可知：在该抛物线上存在一点E，使得以D、E、B、C为顶点的四边形是平行四边形，点E的坐标为（，﹣）、（，）或（﹣，）．
