题目内容
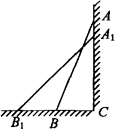
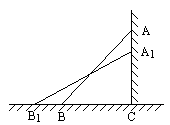
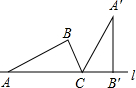 如图Rt△ABC的斜边AC在直线l上,∠BAC=30°,BC=1.若将Rt△ABC以点C为中心顺时针旋转到如图所示位置,则点A运动到点A′所经过的路线长为
如图Rt△ABC的斜边AC在直线l上,∠BAC=30°,BC=1.若将Rt△ABC以点C为中心顺时针旋转到如图所示位置,则点A运动到点A′所经过的路线长为| 4 |
| 3 |
| 4 |
| 3 |
分析:点A运动到点A′所经过的路线是以C为圆心,以AC为半径的弧,求的圆心角∠ACA′,和半径AC即可利用弧长公式求解.
解答:解:∵Rt△ABC中,∠BAC=30°,BC=1,
∴AC=2BC=2.∠ACB=60°
∴∠A′CB′=60°.
∴ACA′=120°.
∴A运动到点A′所经过的路线长是
=
.
∴AC=2BC=2.∠ACB=60°
∴∠A′CB′=60°.
∴ACA′=120°.
∴A运动到点A′所经过的路线长是
| 120π×2 |
| 180 |
| 4π |
| 3 |
点评:本题主要考查了弧长公式,正确求得圆心角以及半径长是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
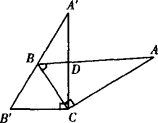
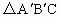 的位置,其中
的位置,其中 分别是A、B对应点,且点B在斜边
分别是A、B对应点,且点B在斜边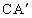 交AB于D,这时∠BDC的度数是
交AB于D,这时∠BDC的度数是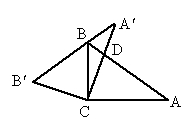

 的位置,其中
的位置,其中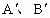 分别是A、B对应点,且点B在斜边
分别是A、B对应点,且点B在斜边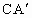 交AB于D,这时∠BDC的度数是
交AB于D,这时∠BDC的度数是