题目内容
(2010•普陀区一模)已知△ABC为等边三角形,AB=6,P是AB上的一个动点(与A、B不重合),过点P作AB的垂线与BC相交于点D,以点D为正方形的一个顶点,在△ABC内作正方形DEFG,其中D、E在BC上,F在AC上,(1)设BP的长为x,正方形DEFG的边长为y,写出y关于x的函数解析式及定义域;
(2)当BP=2时,求CF的长;
(3)△GDP是否可能成为直角三角形?若能,求出BP的长;若不能,请说明理由.

【答案】分析:(1)在△BDP中,根据已知条件得BD=2x,在△CEF中,根据已知条件得EC= ,得y关于x的函数解析式.再求出x的定义域.
,得y关于x的函数解析式.再求出x的定义域.
(2)BP=2,根据(2)得到的y关于x的函数解析式求出CF的长.
(3)假设△GDP是直角三角形,得△APF是直角三角形,得PF的x、y的函数解析式.再把(2)得到的关于x、y的函数解析式代入PF的函数解析式中,得到BP的长.
解答: 解:(1)∵△ABC为等边三角形,
解:(1)∵△ABC为等边三角形,
∴∠B=∠C=60°,AB=BC=AC=6.(1分)
∵DP⊥AB,BP=x,
∴BD=2x.(1分)
又∵四边形DEFG是正方形,
∴EF⊥BC,EF=DE=y,
∴ .(1分)
.(1分)
∴ ,(2分)
,(2分)
∴ .(1分)
.(1分)
(6-3 ≤x<3)(1分)
≤x<3)(1分)
(2)当BP=2时, =
= .(1分)
.(1分)
 .(1分)
.(1分)
(3)△GDP能成为直角三角形.(1分)
①∠PGD=90°时,
 ,
,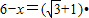
 ,
,
得到: .(2分)
.(2分)
②∠GPD=90°时,G在AB上,参照(1).
点评:此题是一个综合性很强的题目,主要考查等边三角形的性质、解直角三角形、三角形相似、函数等知识.
难度很大,有利于培养同学们钻研和探索问题的精神.
 ,得y关于x的函数解析式.再求出x的定义域.
,得y关于x的函数解析式.再求出x的定义域.(2)BP=2,根据(2)得到的y关于x的函数解析式求出CF的长.
(3)假设△GDP是直角三角形,得△APF是直角三角形,得PF的x、y的函数解析式.再把(2)得到的关于x、y的函数解析式代入PF的函数解析式中,得到BP的长.
解答:
 解:(1)∵△ABC为等边三角形,
解:(1)∵△ABC为等边三角形,∴∠B=∠C=60°,AB=BC=AC=6.(1分)
∵DP⊥AB,BP=x,
∴BD=2x.(1分)
又∵四边形DEFG是正方形,
∴EF⊥BC,EF=DE=y,
∴
 .(1分)
.(1分)∴
 ,(2分)
,(2分)∴
 .(1分)
.(1分)(6-3
 ≤x<3)(1分)
≤x<3)(1分)(2)当BP=2时,
 =
= .(1分)
.(1分) .(1分)
.(1分)
(3)△GDP能成为直角三角形.(1分)
①∠PGD=90°时,
 ,
,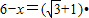
 ,
,得到:
 .(2分)
.(2分)②∠GPD=90°时,G在AB上,参照(1).
点评:此题是一个综合性很强的题目,主要考查等边三角形的性质、解直角三角形、三角形相似、函数等知识.
难度很大,有利于培养同学们钻研和探索问题的精神.

练习册系列答案
相关题目

