题目内容
(2010•普陀区一模)如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(3,0)、B(2,3),C(0,3).(1)求这个二次函数的解析式;
(2)连接AB、AC、BC,求△ABC的面积;
(3)求tan∠BAC的值.

【答案】分析:(1)分别把A(3,0)、B(2,3)、C(0,3)代入y=ax2+bx+c,利用待定系数法可得a=-1,b=2,c=3.故这个二次函数的解析式为:y=-x2+2x+3.
(2)连接AB、AC、BC,利用BC∥OA的性质可知S△ABC=S△OBC=3.
(3)根据Rt△AOC中边长的数量关系可知,∠CAO=∠ACO=45°,则AC=3 .过点BC作BD⊥AC,垂足为D点,S△ABC=3.可求得
.过点BC作BD⊥AC,垂足为D点,S△ABC=3.可求得 .∠BCO=45°,依次求出BD=CD=
.∠BCO=45°,依次求出BD=CD= ,AD=2
,AD=2 ,则tan∠BAC=
,则tan∠BAC= .
.
解答:解:(1)分别把A(3,0)、B(2,3)、C(0,3)
代入y=ax2+bx+c,
得 (1分)
(1分)
解得a=-1,b=2,c=3.(3分)
故这个二次函数的解析式为:y=-x2+2x+3.(1分)
(2)连接AB、AC、BC,如图所示.(1分)
∵BC∥OA,
∴S△ABC=S△OBC= ×2×3=3.
×2×3=3.

(3)在Rt△AOC中,∵AO=3,OC=3,
∴∠CAO=∠ACO=45度.
∴ .
.
(或使用其他锐角三角比或使用勾股定理)(1分)
过点BC作BD⊥AC,垂足为D点,如图.
∵ ,S△ABC=3,
,S△ABC=3,
∴ ,
,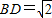 .(1分)
.(1分)
∵BC⊥OC,∠ACO=45°,
∴∠BCO=90°-45°=45°,
∴ ,
, .(1分)
.(1分)
∴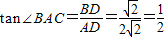 .(1分)
.(1分)
点评:本题考查二次函数的综合应用,其中涉及到的知识点有待定系数法求函数解析式和梯形的性质,三角函数的运用等.要熟练掌握才能灵活运用.
(2)连接AB、AC、BC,利用BC∥OA的性质可知S△ABC=S△OBC=3.
(3)根据Rt△AOC中边长的数量关系可知,∠CAO=∠ACO=45°,则AC=3
 .过点BC作BD⊥AC,垂足为D点,S△ABC=3.可求得
.过点BC作BD⊥AC,垂足为D点,S△ABC=3.可求得 .∠BCO=45°,依次求出BD=CD=
.∠BCO=45°,依次求出BD=CD= ,AD=2
,AD=2 ,则tan∠BAC=
,则tan∠BAC= .
.解答:解:(1)分别把A(3,0)、B(2,3)、C(0,3)
代入y=ax2+bx+c,
得
 (1分)
(1分)解得a=-1,b=2,c=3.(3分)
故这个二次函数的解析式为:y=-x2+2x+3.(1分)
(2)连接AB、AC、BC,如图所示.(1分)
∵BC∥OA,
∴S△ABC=S△OBC=
 ×2×3=3.
×2×3=3.
(3)在Rt△AOC中,∵AO=3,OC=3,
∴∠CAO=∠ACO=45度.
∴
 .
.(或使用其他锐角三角比或使用勾股定理)(1分)
过点BC作BD⊥AC,垂足为D点,如图.
∵
 ,S△ABC=3,
,S△ABC=3,∴
 ,
,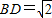 .(1分)
.(1分)∵BC⊥OC,∠ACO=45°,
∴∠BCO=90°-45°=45°,
∴
 ,
, .(1分)
.(1分)∴
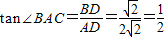 .(1分)
.(1分)点评:本题考查二次函数的综合应用,其中涉及到的知识点有待定系数法求函数解析式和梯形的性质,三角函数的运用等.要熟练掌握才能灵活运用.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目

