题目内容
【题目】如图,在 ![]() 中,AD是高,E、F分别是AB、AC的中点,
中,AD是高,E、F分别是AB、AC的中点,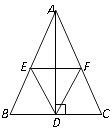
(1)AB=10,AC=8,求四边形AEDF的周长;
(2)EF与AD有怎样的位置关系,证明你的结论.
【答案】
(1)解:∵AB=10,AC=8,E、F分别是AB、AC的中点,
∴AE=![]() AB=5,AF=
AB=5,AF=![]() AC=4.
AC=4.
∵AD是高,
∴AD⊥BC.
∵在Rt△ABD和Rt△ADC中,E、F分别是AB、AC的中点,
∴DE=![]() AB=5,DF=
AB=5,DF=![]() AC=4.
AC=4.
∴C四边形AEDF=AE+ED+DF+AF=5+5+4+4=18.
(2)解:EF垂直平分AD,理由如下:
∵由(1)得AE=DE,AF=DF,
∴E、F在AD的垂直平分线上.
∴EF是AD的垂直平分线 ,
∴EF垂直平分AD 。
【解析】(1)根据中点的定义得出;AE,AF的长,根据直角三角形斜边上的中线等于斜边的一半,分别在Rt△ABD和Rt△ADC中求出ED和DF的长,然后根据四边形的周长计算方法算出结果;
(2)由AE=DE,AF=DF,知E、F在AD的垂直平分线上. 根据垂直平分线的判定定理得出结论。

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目