题目内容
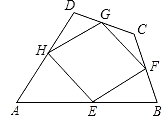
用长度为32m的金属材料制成如图所示的金属框，下部为一个矩形，上部为一个等边三角形．当下部的矩形面积最大时，求矩形的AB、BC的边长各为多少m？并求此时整个金属框的面积是多少？
（1）设AB=x，矩形ABCD的面积为y，则：BC=16-2x
得：y=x×（16-2x）y=-2x2+16x
当x=-
=4时，矩形ABCD的面积有最大值
∴AB=4m，BC=8m
（2）作EH⊥CD，垂足为H
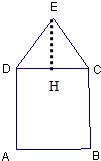
∵△CDE是等边三角形
∴CH=DH=2
∴EH=
CH=2
∴S△CDE=
×4×2
=4
又∵x=-
=4时，y最大值=32
整个金属框的面积=4
+32
得：y=x×（16-2x）y=-2x2+16x
当x=-
| b |
| 2a |
∴AB=4m，BC=8m
（2）作EH⊥CD，垂足为H
∵△CDE是等边三角形
∴CH=DH=2
∴EH=
| 3 |
| 3 |
∴S△CDE=
| 1 |
| 2 |
| 3 |
| 3 |
又∵x=-
| b |
| 2a |
整个金属框的面积=4
| 3 |
练习册系列答案
手拉手全优练考卷系列答案
相关题目
