题目内容
如图⊙O是∆ABC的外接圆,且AB=AC,点D在弧BC上运动,过点D作DE//BC,DE交AB的延长线于点E,连结AD、BD
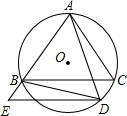
(1)求证∠ADB=∠E;
(2)当点D运动到什么位置时,DE是⊙O的切线?请说明理由;
(3)当AB=5,BC=6时,求⊙O的半径.

(1)求证∠ADB=∠E;
(2)当点D运动到什么位置时,DE是⊙O的切线?请说明理由;
(3)当AB=5,BC=6时,求⊙O的半径.
(1)证明见解析;(2)当点D是弧BC的中点时,DE是⊙O的切线,理由见解析;(3) 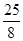 .
.
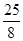 .
.试题分析:(1)运用圆周角定理,以及平行线的性质得出角之间的关系,得出相等关系;
(2)当点D运动到弧BC中点时,DE是⊙O的切线,理由为:由D为弧BC中点,利用垂径定理的逆定理得到AD垂直于BC,且AD过圆心,由BC与DE平行,利用与平行线中的一条垂直,与另一条也垂直得到AD与DE垂直,即可确定出DE为圆的切线.
(3)连接BO,AO,延长AO交BC于点F,由等腰三角形的性质得到AF与BC垂直,且F为BC的中点,求出BF的长,在直角三角形ABF中,理由勾股定理求出AF的长,设圆O的半径为r,在直角三角形OBF中,由AF-AO表示出OF,利用勾股定理列出关于r的方程,求出方程的解即可得到圆的半径长.
试题解析:(1)证明:在∆ABC中,∵AB=AC,∴∠ABC=∠C
∵DE//BC,∴∠ABC=∠E,∴∠E=∠C
∵∠ADB=∠C
∴∠ADB=∠E
(2)当点D是弧BC的中点时,DE是⊙O的切线
理由:当点D是弧BC的中点时,则有AD⊥BC,且AD过圆心O,如图:
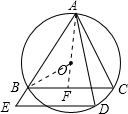
∵DE//BC,∴AD⊥ED
∴DE是⊙O的切线
(3)∵AB=5,∴AF=4
设⊙O的半径为r,在Rt∆OBF中,DF=4-r,OB=r,BF=3.
∴r2=32+(4-r)2,解得r=
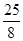
∴⊙O的半径是
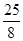 .
.考点: 1.圆周角定理;2.平行线的性质;3.等腰三角形的性质.

练习册系列答案
相关题目
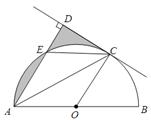
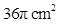
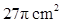
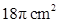
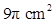
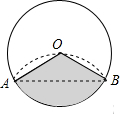
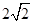
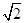
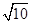
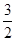
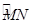 是圆心角为90º的弧,其大小尺寸如图标示.
是圆心角为90º的弧,其大小尺寸如图标示.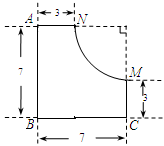
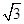 ,则顶点A运动到点A″的位置时.
,则顶点A运动到点A″的位置时.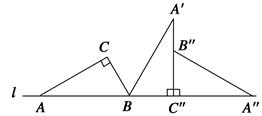
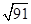 cm2
cm2