题目内容
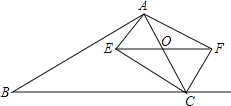
【题目】如图,一张三角形纸片![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,现小林将纸片做三次折叠:第一次使点
,现小林将纸片做三次折叠:第一次使点![]() 落在
落在![]() 处;将纸片展平做第二次折叠,使点
处;将纸片展平做第二次折叠,使点![]() 若在
若在![]() 处;再将纸片展平做第三次折叠,使点
处;再将纸片展平做第三次折叠,使点![]() 落在
落在![]() 处,这三次折叠的折痕长依次记为
处,这三次折叠的折痕长依次记为![]() ,则
,则![]() 的大小关系是(从大到小)__________.
的大小关系是(从大到小)__________.
【答案】b>c>a.
【解析】
由图1,根据折叠得DE是△ABC的中位线,可得出DE的长,即a的长;
由图2,同理可得MN是△ABC的中位线,得出MN的长,即b的长;
由图3,根据折叠得:GH是线段AB的垂直平分线,得出AG的长,再利用两角对应相等证△ACB∽△AGH,利用比例式可求GH的长,即c的长.
解:第一次折叠如图1,折痕为DE,
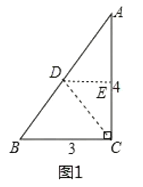
由折叠得:AE=EC=![]() AC=
AC=![]() ×4=2,DE⊥AC
×4=2,DE⊥AC
∵∠ACB=90°
∴DE∥BC
∴a=DE=![]() BC=
BC=![]() ×3=
×3=![]() ,
,
第二次折叠如图2,折痕为MN,
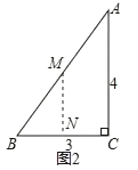
由折叠得:BN=NC=![]() BC=
BC=![]() ×3=
×3=![]() ,MN⊥BC
,MN⊥BC
∵∠ACB=90°
∴MN∥AC
∴b=MN=![]() AC=
AC=![]() ×4=2,
×4=2,
第三次折叠如图3,折痕为GH,
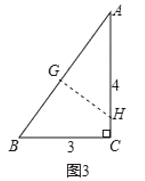
由勾股定理得:AB=![]() =5
=5
由折叠得:AG=BG=![]() AB=
AB=![]() ,GH⊥AB
,GH⊥AB
∴∠AGH=90°
∵∠A=∠A,∠AGH=∠ACB,
∴△ACB∽△AGH
∴![]() ,即
,即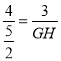 ,
,
∴GH=![]() ,即c=
,即c=![]() ,
,
∵2>![]() >
>![]() ,
,
∴b>c>a,
故答案为:b>c>a.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
【题目】某服装店用6000元购进A,B两种新式服装,按标价售出后可获得毛利润3800元(毛利润=售价﹣进价),这两种服装的进价、标价如下表所示:
类型 价格 | A型 | B型 |
进价(元/件) | 60 | 100 |
标价(元/件) | 100 | 160 |
(1)求这两种服装各购进的件数;
(2)如果A中服装按标价的8折出售,B中服装按标价的7折出售,那么这批服装全部售完后,服装店比按标价售出少收入多少元?