题目内容
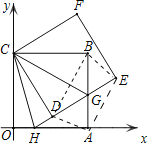
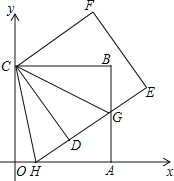
【题目】如图，正方形ABCO的边OA、OC在坐标轴上，点B坐标为（8，8），将正方形ABCO绕点C逆时针旋转角度α（0°＜α＜90°），得到正方形CDEF，ED交线段AB于点G，ED的延长线交线段OA于点H，连CH、CG．
（1）求证：△CBG≌△CDG；
（2）求∠HCG的度数；判断线段HG、OH、BG的数量关系，并说明理由；
（3）连结BD、DA、AE、EB得到四边形AEBD，在旋转过程中，四边形AEBD能否为矩形？如果能，请求出点H的坐标；如果不能，请说明理由．
【答案】（1）见解析；（2）HG=HD+DG=HO+BG；（3）H点的坐标为（2，0）．
【解析】
试题分析：（1）求证全等，观察两个三角形，发现都有直角，而CG为公共边，进而再锁定一条直角边相等即可，因为其为正方形旋转得到，所以边都相等，即结论可证．
（2）根据（1）中三角形全等可以得到对应边、角相等，即BG=DG，∠DCG=∠BCG．同第一问的思路容易发现△CDH≌△COH，也有对应边、角相等，即OH=DH，∠OCH=∠DCH．于是∠GCH为
四角的和，四角恰好组成直角，所以∠GCH=90°，且容易得到OH+BG=HG．
（3）四边形AEBD若为矩形，则需先为平行四边形，即要对角线互相平分，合适的点只有G为AB中点的时候．由上几问知DG=BG，所以此时同时满足DG=AG=EG=BG，即四边形AEBD为矩形．求H点的坐标，可以设其为（x，0），则OH=x，AH=6﹣x．而BG为AB的一半，所以DG=BG=AG=3．又由（2），HG=x+3，所以Rt△HGA中，三边都可以用含x的表达式表达，那么根据勾股定理可列方程，进而求出x，推得H坐标．
（1）证明：∵正方形ABCO绕点C旋转得到正方形CDEF，
∴CD=CB，∠CDG=∠CBG=90°．
在Rt△CDG和Rt△CBG中，
，
∴△CDG≌△CBG（HL）；
（2）解：∵△CDG≌△CBG，
∴∠DCG=∠BCG，DG=BG．
在Rt△CHO和Rt△CHD中，
∵
，
∴△CHO≌△CHD（HL），
∴∠OCH=∠DCH，OH=DH，
∴∠HCG=∠HCD+∠GCD=∠OCD+∠DCB=
∠OCB=45°，
∴HG=HD+DG=HO+BG；
（3）解：四边形AEBD可为矩形．
如图，连接BD、DA、AE、EB，四边形AEBD若为矩形，则需先为平行四边形，即要对角线互相平分，合适的点只有G为AB中点的时候．
∵DG=BG，
∴DG=AG=EG=BG，即平行四边形AEBD对角线相等，则其为矩形，
∴当G点为AB中点时，四边形AEBD为矩形．
∵四边形DAEB为矩形，
∴AG=EG=BG=DG．
∵AB=6，
∴AG=BG=3．
设H点的坐标为（x，0），则HO=x
∵OH=DH，BG=DG，
∴HD=x，DG=3．
在Rt△HGA中，
∵HG=x+3，GA=3，HA=6﹣x，
∴（x+3）2=32+（6﹣x）2，解得x=2．
∴H点的坐标为（2，0）．
