Question

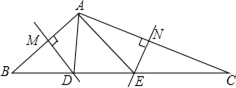
【题目】如图，在△ABC中，边AB、AC的垂直平分线分别交BC于D、E．

（1）若BC=5，求△ADE的周长．

（2）若∠BAC=120°，求∠DAE的度数．

Answer 1

【答案】（1）5;(2)60°

【解析】（1）根据线段垂直平分线的性质得到DA=DB，EA=EC，根据三角形的周长公式计算即可；

（2）根据三角形内角和定理求出∠B+∠C=60°，根据等边对等角、结合图形计算即可．

（1）∵边AB、AC的垂直平分线分别交BC于D、E，∴DA=DB，EA=EC，∴△ADE的周长=AD+DE+AE=DB+DE+EC=BC=5；

（2）∵∠BAC=120°，∴∠B+∠C=60°．

∵DA=DB，EA=EC，∴∠DAB=∠B，∠EAC=∠C，∴∠DAE=∠BAC﹣（∠DAB+∠EAC）=∠BAC﹣（∠B+∠C）=60°．